



Siguiente: Segundas listas
Arriba: Códigos lineales
Anterior: Pesos mínimos
Sea 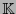 un campo finito y sea
un campo finito y sea  un código lineal-
un código lineal-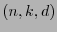 .
Al ser
.
Al ser  un subespacio, el cociente
un subespacio, el cociente
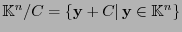 es a su vez un espacio vectorial sobre
es a su vez un espacio vectorial sobre 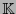 . Naturalmente, dos palabras cualesquiera
. Naturalmente, dos palabras cualesquiera
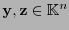 en una misma clase del cociente
en una misma clase del cociente
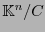 , es decir, tales que
, es decir, tales que
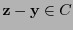 , han de poseer el mismo síndrome:
, han de poseer el mismo síndrome:
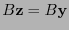 donde
donde
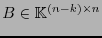 es la matriz revisora de paridad de
es la matriz revisora de paridad de  .
.
También, si al transmitir una palabra en el código, digamos 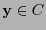 , se recibiera la palabra
, se recibiera la palabra
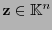 entonces para el error
entonces para el error
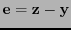 se habría de tener
se habría de tener
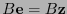 . Así pues, el síndrome del error ha de coincidir con el síndrome de la palabra recibida, lo que, por lo anterior, equivale a que la palabra recibida
. Así pues, el síndrome del error ha de coincidir con el síndrome de la palabra recibida, lo que, por lo anterior, equivale a que la palabra recibida 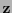 y el error cometido
y el error cometido 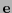 necesariamente han de estar en una misma clase lateral de
necesariamente han de estar en una misma clase lateral de
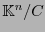 .
.
Definición 5.7
Para cada clase
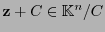 , un representante principal de ella es un vector
, un representante principal de ella es un vector
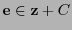 de peso de Hamming mínimo.
de peso de Hamming mínimo.
Por el Teorema Fundamental de Homomorfismos se tiene que
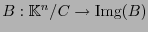 es un isomorfismo. Así, para cada posible valor de síndrome
es un isomorfismo. Así, para cada posible valor de síndrome
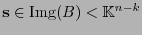 existe una única clase lateral
existe una única clase lateral
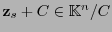 tal que
tal que
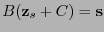 . Sea
. Sea 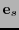 un representante principal de la clase
un representante principal de la clase 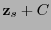 . Resulta entonces un
. Resulta entonces un
- Procedimiento de decodificación.
- Supóngase que al transmitir una palabra
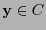 se recibe la palabra
se recibe la palabra
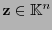 cometiéndose el error
cometiéndose el error
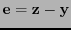 . Entonces se calcula el síndrome
. Entonces se calcula el síndrome
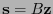 y, considerando el representante principal
y, considerando el representante principal 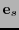 , se recupera la palabra transmitida tomando
, se recupera la palabra transmitida tomando
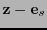 .
.
Este procedimiento es, claramente, correcto toda vez que
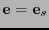 . Una manera de sistematizarlo es la siguiente:
. Una manera de sistematizarlo es la siguiente:
Utilizando el arreglo estándar se tiene el siguiente:
- Procedimiento de decodificación.
- Supóngase que al transmitir una palabra
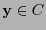 se recibe la palabra
se recibe la palabra
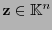 cometiéndose el error
cometiéndose el error
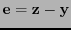 . Entonces se localiza en
. Entonces se localiza en 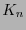 los índices
los índices 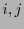 tales que
tales que
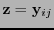 , y se toma a
, y se toma a
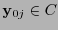 como la palabra original
como la palabra original 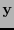 .
.
Este procedimiento es, claramente, correcto toda vez que el error 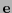 coincida con el representante principal
coincida con el representante principal 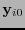 de la clase
de la clase 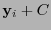 en la que apareció
en la que apareció 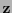 .
.




Siguiente: Segundas listas
Arriba: Códigos lineales
Anterior: Pesos mínimos
Guillermo M. Luna
2010-05-09
![]() un campo finito y sea
un campo finito y sea ![]() un código lineal-
un código lineal-![]() .
Al ser
.
Al ser ![]() un subespacio, el cociente
un subespacio, el cociente
![]() es a su vez un espacio vectorial sobre
es a su vez un espacio vectorial sobre ![]() . Naturalmente, dos palabras cualesquiera
. Naturalmente, dos palabras cualesquiera
![]() en una misma clase del cociente
en una misma clase del cociente
![]() , es decir, tales que
, es decir, tales que
![]() , han de poseer el mismo síndrome:
, han de poseer el mismo síndrome:
![]() donde
donde
![]() es la matriz revisora de paridad de
es la matriz revisora de paridad de ![]() .
.
![]() , se recibiera la palabra
, se recibiera la palabra
![]() entonces para el error
entonces para el error
![]() se habría de tener
se habría de tener
![]() . Así pues, el síndrome del error ha de coincidir con el síndrome de la palabra recibida, lo que, por lo anterior, equivale a que la palabra recibida
. Así pues, el síndrome del error ha de coincidir con el síndrome de la palabra recibida, lo que, por lo anterior, equivale a que la palabra recibida ![]() y el error cometido
y el error cometido ![]() necesariamente han de estar en una misma clase lateral de
necesariamente han de estar en una misma clase lateral de
![]() .
.
![]() es un isomorfismo. Así, para cada posible valor de síndrome
es un isomorfismo. Así, para cada posible valor de síndrome
![]() existe una única clase lateral
existe una única clase lateral
![]() tal que
tal que
![]() . Sea
. Sea ![]() un representante principal de la clase
un representante principal de la clase ![]() . Resulta entonces un
. Resulta entonces un