Siguiente: Programas Arriba: Segundas listas Anterior: Segundas listas

Ejercicios

1. Verifique que las tablas siguientes definen una estructura de campo en el conjunto de 4 elementos $F=\{0,1,p,q\}$:

$$\begin{array}{cc} \begin{array}{c\vert cccc} + & 0 & 1 & p & ... ... & 0 & p & q & 1 \\ q & 0 & q & 1 & p \end{array} \end{array}$$

Indique cómo se puede extender esas tablas de manera que determinen un campo de 8 elementos.

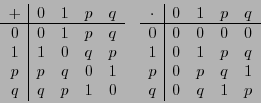
2. El polinomio $p(X)= 1+X^2+X^5$ es irreducible en $\mathbb{F}_2[X]$. Describa la tabla de adición y de multiplicación del cociente $\mathbb{F}_2[X]/(p(X))$.

3. Demuestre que el conjunto $\mathbb{K}^{m\times n}$, de matrices de orden $m\times n$ y entradas en un campo $\mathbb{K}$, es un espacio vectorial sobre $\mathbb{K}$. Determine la dimensión de $\mathbb{K}^{m\times n}$.

4. Sea $C$ un código-$[n,k]$ binario. Suponga que la distancia mínima de $C$ es bien $2t$ o bien $2t+1$ y que se está usando un canal simétrico con probabilidad de error $p$. Muestre que la probabilidad de error en el código satisface $P_{err}(C)\leq \sum_{j=t+1}^n{n\choose j} p^j(1-p)^{n-j}$.

5. Suponga un canal simétrico con probabilidad de error $p=10^{-1}$. ¿Cuál debería ser el tamaño de $n$ para que en el código de $n$ repeticiones de cada bit se tenga $P_{err}(C)\leq 10^{-4}$?

6. Si $\sigma = s_0\cdots s_{n-1}\in\{0,1\}^*$ es una palabra binaria su reverso es la palabra $\mbox{rev}(\sigma) = s_{n-1}\cdots s_0\in\{0,1\}^*$. El conjunto de $n$-palíndromas es $P_n=\{\sigma\in\{0,1\}^n\vert\, \sigma = \mbox{rev}(\sigma)\}$ que consta de las palabras de longitud $n$ que se leen iguales en cualquier sentido. Decida si $P_n$ es un código lineal, y si lo fuera determine un conjunto de ecuaciones para determinar cuándo una palabra cae en el código. Calcule la distancia mínima de este código y diga cuántos errores de bits puede detectar.

7. Describa un procedimiento para detectar errores triples cuando se utiliza un código recangular $5\times 2$.

8. Sea $\mathbb{F}_p^n$ el espacio de dimensión $n$ sobre el campo $\mathbb{F}_p$, donde $p$ es un número primo. Para cada entero $k\leq n$ cuente cuántos subespacios de dimensión $k$ hay en $\mathbb{F}_p^n$.

9. Pruebe que la decodificación de un código de Hamming es siempre incorrecta si hay dos bits erróneos en una misma palabra de código.

10. Considere el código lineal $C\subset\mathbb{F}_2^n$ determinado por el sistema de ecuaciones

$$\begin{eqnarray*} X_4 &=& X_1 + X_2 + X_3 \\ X_5 &=& X_0 + X_1 + X_2 \\ X_6 &=& X_0 + X_1 + X_4 \\ X_7 &=& X_0 + X_2 + X_3 %\\ \end{eqnarray*}$$

Calcule una matriz de paridad y verifique que la distancia mínima es 3.

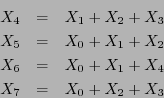
11. En el espacio $\mathbb{F}_2^n$ sea $C_0$ el código consistente de los vectores con peso de Hamming par. Encuentre una matriz generatriz y una revisora de paridad y calcule la distancia mínima.

12. ¿Cómo son los códigos en $\mathbb{F}_2^n$ cuyas matrices generatrices son invertibles?

13. Muestre que los triángulos equiláteros en un espacio vectorial $\mathbb{F}_2^n$ tienen aristas pares. En otras palabras, muestre que si ${\bf x}_0,{\bf x}_1,{\bf x}_2\in\mathbb{F}_2^n$ son tales que la distancia entre cualesquiera dos de ellos es $d\in\mathbb{N}$, entonces $d$ es un número par. Muestre que en tal caso hay un único punto ${\bf c}\in\mathbb{F}_2^n$ cuya distancia a cada ${\bf x}_i$ es $d/2$. Es decir, todo triángulo equilátero posee un centro.

14. Sea $C$ un código lineal binario. Muestre que bien todas las palabras en $C$ comienzan con $0$ o bien exactamente una mitad del código consta de palabras que comienzan con $0$.

15. En el espacio $\mathbb{F}_2^n$ sea $C_1=\{0^n,1^n\}$ el código con sólo dos palabras: las constantes 0 y 1. Encuentre una matriz generatriz y una revisora de paridad y calcule la distancia mínima.

16. Sea $C$ un código lineal en el espacio $\mathbb{F}_2^n$. Para cada ${\bf x}\in\mathbb{F}_2^n$, denotemos por ${\bf x}+ C$ a la clase lateral en $\mathbb{F}_2^n/C$ que contiene a ${\bf x}$.

Muestre que si ${\bf y}\in{\bf x}+ C$ entonces ${\bf y}+ C={\bf x}+ C$, y si ${\bf y}\not\in{\bf x}+ C$ entonces $\left({\bf y}+ C\right)\cap\left({\bf x}+ C\right) = \emptyset$.

17. Sea $C$ un código lineal en el espacio $\mathbb{F}_2^n$. Muestre que $C\cup({\bf x}+ C)$ también es un código lineal en el espacio $\mathbb{F}_2^n$.

18. Pruebe que los códigos- $(2^n-1,2^n-n-1,3)$ de Hamming son perfectos.

19. Un código lineal-$(n,k)$ $C$ se dice ser autodual si $C=C^{\perp}$. Muestre que un código lineal-$(n,k)$ $C$ en el espacio $\mathbb{F}_2^n$ es autodual si y sólo si cualesquiera dos renglones en una matriz generatriz de $C$ son ortogonales (su producto interno es cero) y $k=\frac{n}{2}$.

20. Sea $H\in\mathbb{F}_2^{(n-k)\times n}$ la matriz revisora de paridad de un código-$[n,k]$ $C$ cuyo peso mínimo es un entero impar. Construya un nuevo código $D$ cuya matriz revisora de paridad es

$$\overline{H}=\left[\begin{array}{ll} H & 1^{(n-k)} \\ \left(0^{(n)}\right)^T & 1 \end{array}\right].$$

Muestre que $D$ es un código-$[n+1,k]$ cuyo peso mínimo es $d+1$.

Siguiente: Programas Arriba: Segundas listas Anterior: Segundas listas