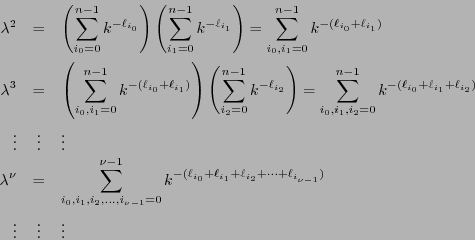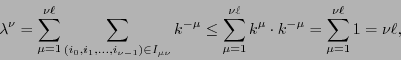Siguiente: Algoritmo de Sardinas-Patterson Arriba: Codificación Anterior: Funciones de codificación

Decodificación única

Teorema 2.1 (Kraft)   Sea $A = \left\{a_i\right\}_{i=0}^{n-1}$ un alfabeto de $n$ símbolos y sea $L = \left\{\ell_i\right\}_{i=0}^{n-1}$ un conjunto de $n$ números naturales distintos de cero. Existe un código instantáneo, utilizando un alfabeto de código $C$ de $k$ símbolos, de manera que cada $a_i$ corresponda a una palabra de longitud $\ell_i$ cuando y sólo cuando se cumpla la desigualdad de Kraft

$$\sum_{i=0}^{n-1} k^{-\ell_i} \leq 1.$$ (1)

En efecto, haciendo un renombramiento de símbolos si fuera necesario, podemos suponer que 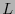$L$ es no-decreciente: $1\leq \ell_0 \leq \ell_1 \leq \cdots \leq \ell_{n-1}.$

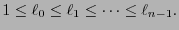
Supongamos que existe un código instantáneo 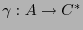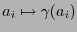$\gamma: A\to C^*$, $a_i \mapsto \gamma(a_i)$, tal que

$$\mbox{\rm long}\left(\gamma(a_i)\right)=\ell_i\ , \ 0\leq i\leq n-1.$$

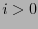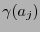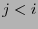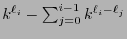Al ser el código instantáneo, para cada $i>0$, ningún $\gamma(a_{j})$, con $j<i$, puede ser un prefijo de $\gamma(a_i)$. Así pues, se tiene exactamente $k^{\ell_i} - \sum_{j=0}^{i-1}k^{\ell_i - \ell_{j}}$ posibilidades de elegir $\gamma(a_i)$. En consecuencia,

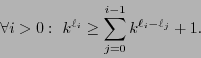$$\forall i>0:\ k^{\ell_i} \geq \sum_{j=0}^{i-1}k^{\ell_i - \ell_{j}} +1.$$ (2)

En particular, para 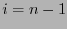$i=n-1$, al dividir ambos miembros de la desigualdad (2) entre 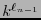$k^{\ell_{n-1}}$ resulta la desigualdad de Kraft (1).

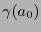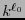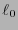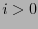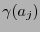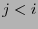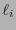Recíprocamente suponiendo que vale (1) entonces puede verse consecutivamente que valen las relaciones (2). El código instantáneo se construye de manera sucesiva: Para $\gamma(a_0)$ elíjase una de las $k^{\ell_{0}}$ palabras posibles de longitud $\ell_{0}$. Para cada $i>0$ habiendo construído $\gamma(a_{j})$, con $j<i$, elíjase como $\gamma(a_i)$ a una palabra de longitud $\ell_{i}$ que no tenga como prefijo a ninguna 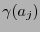$\gamma(a_{j})$. Por la desigualdad (2), esto último siempre es posible. $\Box$

Teorema 2.2 (McMillan)   Cualquier código de decodificación única satisface la desigualdad de Kraft.

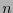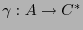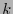Sea $A = \left\{a_i\right\}_{i=0}^{n-1}$ un alfabeto de $n$ símbolos y sea $\gamma: A\to C^*$ una codificación de decodificación única, sobre un alfabeto $C$ de $k$ símbolos. Sea 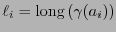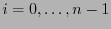$\ell_i=\mbox{\rm long}\left(\gamma(a_i)\right)$, $i=0,\ldots,n-1$. Escribamos 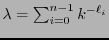$\lambda = \sum_{i=0}^{n-1} k^{-\ell_i}$ y mostremos que, en efecto, 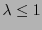$\lambda\leq 1$. Para esto deberemos demostrar que la sucesión 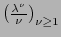$\left(\frac{\lambda^{\nu}}{\nu}\right)_{\nu\geq 1}$ está acotada superiormente (obviamente vale la implicación: 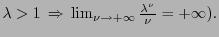$\lambda>1\, \Rightarrow\, \lim_{\nu\to+\infty}\frac{\lambda^{\nu}}{\nu} = +\infty).$ Calculemos entonces las potencias de $\lambda$:

$$\begin{eqnarray*} \lambda^2 &=& \left(\sum_{i_0=0}^{n-1} k^{-\ell_{i_0}}\right) ... ...}+\ell_{i_2}+\cdots+\ell_{i_{\nu-1}})}\\ \vdots &\vdots& \vdots \end{eqnarray*}$$

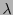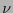Ahora bien, para cada entero $\mu\in\mathbb{N}$ que se realice como la suma de $\nu$ logitudes, sea

$$I_{\mu\nu} = \left\{(i_0,i_1,i_2,\ldots,i_{\nu-1}) \vert\mu=\ell_{i_0}+\ell_{i_1}+\ell_{i_2}+\cdots+\ell_{i_{\nu-1}}\right\}$$

el conjunto de formas de expresar a 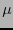$\mu$ como una tal suma y sea

$$S_{\mu\nu}=\{\sigma\in A^{\nu}\vert\gamma^*(\sigma)\in C^{\mu... ..._{i_{\nu-1}}\vert(i_0,i_1,i_2,\ldots,i_{\nu-1})\in I_{\mu\nu}\}$$

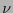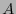el conjunto de palabras de longitud $\nu$ en $A$ que quedan codificadas por palabras de longitud 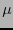$\mu$ en $C$. Ya que el código es de decodificación única, se tiene

$$\mbox{\rm card}(I_{\mu\nu}) = \mbox{\rm card}(S_{\mu\nu}) \leq \mbox{\rm card}(C^{\mu}) = k^{\mu}.$$

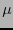Sea $\ell = \max\left[\ell_i\right]_{i=0}^{n-1}$ la mayor de las longitudes de códigos de símbolos. Naturalmente, el mayor de los valores $\mu$ tales que 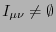$I_{\mu\nu}\not=\emptyset$ es precisamente 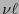$\nu\ell$. En consecuencia:

$$\lambda^{\nu} = \sum_{\mu=1}^{\nu\ell} \sum_{(i_0,i_1,\ldots,... ...l} k^{\mu} \cdot k^{-\mu} = \sum_{\mu=1}^{\nu\ell} 1 = \nu\ell,$$

de donde resulta 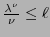$\frac{\lambda^{\nu}}{\nu} \leq \ell$, y esto ocurre para cualquier $\nu$. $\Box$

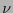Como una consecuencia directa de ambos teoremas, resulta el

Corolario 2.1   Todo código de decodificación única da origen a códigos instantáneos que preservan las longitudes de los códigos asociados a los símbolos.

Siguiente: Algoritmo de Sardinas-Patterson Arriba: Codificación Anterior: Funciones de codificación