 |
[[8] [9]] |
[5] |
[6] |
[2] |
[3] |
[0] |
[1] |
[4] |
[7] |
 |
3 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
 |
[6] |
[2] |
[[[8] [9]] [5]] |
[3] |
[0] |
[1] |
[4] |
[7] |
 |
4 |
5 |
6 |
6 |
7 |
8 |
9 |
10 |
|
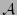 |
[[[8] [9]] [5]] |
[3] |
[0] |
[1] |
[[6] [2]] |
[4] |
[7] |
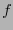 |
6 |
6 |
7 |
8 |
9 |
9 |
10 |
|
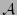 |
[0] |
[1] |
[[6] [2]] |
[4] |
[7] |
[[[[8] [9]] [5]] [3]] |
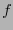 |
7 |
8 |
9 |
9 |
10 |
12 |
|
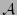 |
[[6] [2]] |
[4] |
[7] |
[[[[8] [9]] [5]] [3]] |
[[0] [1]] |
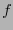 |
9 |
9 |
10 |
12 |
15 |
|
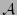 |
[7] |
[[[[8] [9]] [5]] [3]] |
[[0] [1]] |
[[[6] [2]] [4]] |
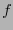 |
10 |
12 |
15 |
18 |
|
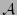 |
[[0] [1]] |
[[[6] [2]] [4]] |
[[7] [[[[8] [9]] [5]] [3]]] |
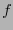 |
15 |
18 |
22 |
|
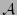 |
[[7] [[[[8] [9]] [5]] [3]]] |
[[[0] [1]] [[[6] [2]] [4]]] |
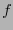 |
22 |
33 |
|
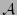 |
[[[7] [[[[8] [9]] [5]] [3]]] [[[0] [1]] [[[6] [2]] [4]]]] |
|
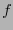 |
55 |
|
|
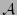 a sus primeras dos componentes. Estas son ``hojas'' o subárboles binarios,
a sus primeras dos componentes. Estas son ``hojas'' o subárboles binarios, 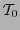 y
y 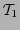 .
.
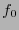 y
y 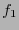 las etiquetas de sus raices.
las etiquetas de sus raices.
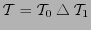 el árbol binario cuyo subárbol izquierdo es
el árbol binario cuyo subárbol izquierdo es 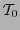 y el derecho es
y el derecho es 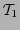 . Etiquétese a su raíz con la suma
. Etiquétese a su raíz con la suma
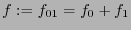 , a su arista izquierda con
, a su arista izquierda con 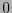 y a su arista derecha con
y a su arista derecha con 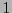 .
.
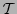 dentro de la lista
dentro de la lista 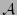 en el lugar que le corresponde según
en el lugar que le corresponde según 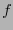 , es decir, en la primera posición tal que todos los elementos de
, es decir, en la primera posición tal que todos los elementos de 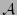 hasta esa posición, tienen un peso estrictamente menor que
hasta esa posición, tienen un peso estrictamente menor que 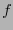 .
.
![\begin{table}\begin{eqnarray*}
\ [\mbox{\it 7}] &\leadsto& 00 \\
\ [\mbox{\it 4...
... algoritmo lograr\'\i a la monoton\'\i a.\end{minipage}\end{center}
\end{table}](img151.png)