Resultantes

Seguiremos aquí la presentación en [1].

Sea $\mathbb{C}$ el campo de los números complejos y sean

$$P(X) = \sum_{i=0}^ma_iX^i , Q(X) = \sum_{j=0}^nb_jX^j\in\mathbb{C}[X]$$ (1)

dos polinomios de grados $m$ y $n$ respectivamente. Sea $M_{P(X),Q(X)}\in\mathbb{C}^{(n+m)\times(m+n)}$ la matriz con entrada general $m_{ij}$ , $i,j\in[\![0,m+n-1]\!]$ , donde

$$m_{ij} = \left\{\begin{array}{ll} a_{m-(i-j)} & \mbox{si }0\leq j... ... \& j-n \leq i\leq j \\ 0 & \mbox{en cualquier otro caso} \end{array}\right.$$

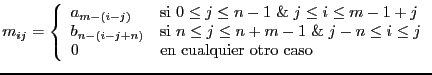
es decir, si se define

$$M_{P(X),n} = \left[\begin{array}{lllcl} a_m & 0 & 0 & \cdots & 0 ... ..._1 \\ 0 & 0 & 0 & \cdots & a_0 \end{array}\right]\in\mathbb{K}^{(m+n)\times n}$$

entonces $M_{P(X),Q(X)} = \left[M_{P(X),n} M_{Q(X),m}\right].$ El resultante de $P(X)$ y $Q(X)$ es

$$(P(X),Q(X)) = \det M_{P(X),Q(X)}\in\mathbb{C}.$$ (2)

Proposición 1.1   Las siguientes propiedades son verdaderas:

Conmutatividad signada.

Res$(P(X),Q(X)) = (-1)^{mn}$Res$(Q(X),P(X))$ .

En términos de las raíces.

Si $x_0,\ldots,x_{m-1}$ son las raíces de $P(X)$ y $y_0,\ldots,y_{n-1}$ son las de $Q(X)$ entonces

Res$$(P(X),Q(X)) = a_mb_n\prod_{i=0}^{m-1}\prod_{j=0}^{n-1}(x_i-y_j) = a_m\prod_{i=0}^{m-1}Q(x_i) = (-1)^{mn} b_n\prod_{j=0}^{n-1}P(y_j).$$

Forma polinomial entera.

Res$(P(X),Q(X))$ está dado mediante un polinomio de coeficientes enteros respecto a los coeficientes de $P(X)$ y $Q(X)$ .

Factor común.

Res$(P(X),Q(X))=0$ cuando y sólo cuando $P(X)$ y $Q(X)$ poseen un factor común no-trivial en $\mathbb{K}[X]$ .

Eliminación.

Res$(P(X),Q(X))$ , visto como un polinomio constante, es una combinación lineal de $P(X)$ y $Q(X)$ con coeficientes en $\mathbb{C}[X]$ dados como polinomios de coeficientes enteros respecto a los coeficientes de $P(X)$ y $Q(X)$ .

Otra caracterización del resultante es la siguiente: Para un polinomio $P(X)\in\mathbb{C}[X]$ sea $\mathbb{C}[X]/(P(X))$ su anillo de residuos. Sea $h_{Q(X)}:\mathbb{C}[X]/(P(X))\to\mathbb{C}[X]/(P(X))$ la homotecia $[R(X)]\mapsto [Q(X) R(X)]$ . Entonces:

$$(P(X),Q(X))=a_m \det(h_{Q(X)}).$$ (3)

Ahora, sean

$$F_P(X,Y) = \sum_{i=0}^ma_iX^iY^{m-i} , F_Q(X,Y) = \sum_{j=0}^nb_jX^jY^{n-j}\in\mathbb{C}[X,Y]$$ (4)

dos polinomios homogéneos en $\mathbb{C}[X,Y]$ . Si $P(X)$ y $Q(X)$ están definidos como en (1), entonces se tiene

$$F_P(X,Y) = Y^m P\left(\frac{X}{Y}\right) , F_Q(X,Y) = Y^n Q\left(\frac{X}{Y}\right),$$ (5)

por lo que se dice que $F_P(X,Y)$ y $F_Q(X,Y)$ se obtienen por homogenización a partir de $P(X)$ y $Q(X)$ mediante (5). En este caso, se define

$$(F_P(X,Y),F_Q(X,Y)) = (P(X),Q(X)) = \det M_{P(X),Q(X)}$$ (6)

(véase la ec. (5)). De acuerdo con la relación nombrada ``Factor común'' en la proposición 1.1, se tiene:

Observación 1.1   Res$(F_P(X,Y),F_Q(X,Y)) = 0$ cuando y sólo cuando el sistema de ecuaciones $F_P(X,Y)=0$ , $F_Q(X,Y)=0$ tiene soluciones no-triviales, es decir, en $\mathbb{C}-\{(0,0)\}$ .

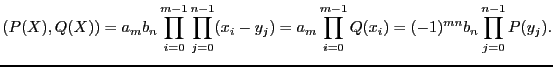
Ahora, para cada $n\in\mathbb{N}$ sea ${\bf X}_{n+1}=(X_0,\cdots,X_n)$ una colección de $n+1$ indeterminadas. Sea $\left(F_i({\bf X}_{n+1})\right)_{i=0}^n$ una colección de $(n+1)$ polinomios homogéneos en $\mathbb{C}[{\bf X}_{n+1}]$ , cada uno $F_i({\bf X}_{n+1})$ de grado total, digamos, $d_i$ , escribamos $F_i({\bf X}_{n+1}) = \sum_{{\bf e}\in I} a_{i,{\bf e}}{\bf X}^{\bf e}$ , con $I_i= \{{\bf e}\in[\![0,n]\!]\vert \sum_{j=0}^n e_j = d_i\}$ y ${\bf X}^{\bf e} = \prod_{j=0}^n X_j^{e_j}$ . Consideremos el sistema de $(n+1)$ ecuaciones con $(n+1)$ incógnitas:

$$\forall i\in[\![0,n]\!]: F_i({\bf X}_{n+1}) = 0$$ (7)

y veamos bajo cuáles condiciones éste posee una solución no-trivial ${\bf x}\in\mathbb{C}^{n+1}-\{{\bf0}\}$ .

Por supuesto, si $\forall i\in[\![0,n]\!]$ , $d_i=1$ , entonces la Regla de Cramer da condiciones para que el sistema (7) posea soluciones no-triviales: $\det\left[a_{i,\{j\}}\right]_{i,j\in[\![0,n+1]\!]}\not=0$ .

Para cada $i\in[\![0,n]\!]$ y cada ${\bf e}\in I_i$ remplacemos el coeficiente $a_{i,{\bf e}}$ por una indeterminada $A_{i,{\bf e}}$ y sea ${\bf A} = \bigcup_{ i\in[\![0,n]\!]}\{A_{i,{\bf e}}\vert {\bf e}\in I_i\}$ . Para un polinomio $P({\bf A})\in\mathbb{Z}[{\bf A}]$ denotemos por $P\left(\left(F_i({\bf X}_{n+1})\right)_{i=0}^n)\right)$ el valor que se obtiene mediante la sustitución $A_{i,{\bf e}}=a_{i,{\bf e}}$ , para todos $i\in[\![0,n]\!]$ y ${\bf e}\in I_i$ . Se dice, por todo esto, que $P({\bf A})$ es un polinomio entero respecto a los coeficientos de los polinomios homogéneos $\left(F_i({\bf X}_{n+1})\right)_{i=0}^n$ .

Proposición 1.2   Fijo un vector de grados ${\bf d} = (d_0,\ldots,d_n)\in(\mathbb{Z}^+)^{n+1}$ existe un único polinomio Res$_{{\bf d}}({\bf A})\in\mathbb{Z}[{\bf A}]$ tal que:

• Si $\left(F_i({\bf X}_{n+1})\right)_{i=0}^n\subset\mathbb{C}[{\bf X}_{n+1}]$ es una colección de polinomios homogéneos, cada uno de grado $d_i$ , entonces el sistema (7) posee soluciones no-triviales cuando y sólo cuando Res$_{{\bf d}}\left(\left(F_i({\bf X}_{n+1})\right)_{i=0}^n)\right)=0$ .
• Si $\forall i\in[\![0,n]\!]$ , $F_i({\bf X}_{n+1}) = X_i^{d_i}$ , entonces Res$_{{\bf d}}\left(\left(F_i({\bf X}_{n+1})\right)_{i=0}^n)\right)=1$ .
• Res$_{{\bf d}}({\bf A})$ es un polinomio irreducible aún cuando se le ve como uno en $\mathbb{C}[{\bf A}]$ .

El valor Res$_{{\bf d}}\left(\left(F_i({\bf X}_{n+1})\right)_{i=0}^n)\right)$ se dice ser el resultante multipolinomial de los polinomios homogéneos $\left(F_i({\bf X}_{n+1})\right)_{i=0}^n$ . Se tiene:

• Para $n=1$ , Res$_{{\bf d}}(F_0(X,Y),F_1(X,Y))$ coincide con Res$(F_0(X,Y),F_1(X,Y))$ definido por la ec. (6).
• Por la regla de Cramer, si ${\bf d}=(1,\ldots,1)\in(\mathbb{Z}^+)^{n+1}$ entonces Res$_{{\bf d}}({\bf A}) = \det\left[a_{i,\{j\}}\right]_{i,j\in[\![0,n+1]\!]}$ .
• Para $n=2$ y ${\bf d}=(2,2,2)\in(\mathbb{Z}^+)^3$ , considerando las formas cuadráticas
  

  $$F_0(X_0,X_1,X_2) = a_{00}X_0^2 + a_{01}X_1^2 + a_{02}X_2^2 + a_{03}X_0X_1 + a_{04}X_0X_2 + a_{05}X_1X_2$$

  $$F_1(X_0,X_1,X_2) = a_{10}X_0^2 + a_{11}X_1^2 + a_{12}X_2^2 + a_{13}X_0X_1 + a_{14}X_0X_2 + a_{15}X_1X_2$$

  $$F_2(X_0,X_1,X_2) = a_{20}X_0^2 + a_{21}X_1^2 + a_{22}X_2^2 + a_{23}X_0X_1 + a_{24}X_0X_2 + a_{25}X_1X_2$$

  
  el resultante tripolinomial Res$_{(2,2,2)}(F_0(X_0,X_1,X_2),F_1(X_0,X_1,X_2),F_2(X_0,X_1,X_2))$ posee 18 variables (los coeficientes $a_{ij}$ , $(i,j)\in[\![0,2]\!]\times[\![0,5]\!]$ ), grado 12 e involucra $21894$ monomios. De hecho, al considerar el jacobiano
  $$J(X_0,X_1,X_2) = \det\left(\left.\frac{\partial F_i}{\partial X_j}\right\vert _{(X_0,X_1,X_2)} \right)_{i,j\in[\![0,2]\!]}$$
  éste determina un polinomio homogéneo de grado 3, y en consecuencia sus derivadas parciales también lo son, pero de grado 2. Al escribir
  

  $$\frac{\partial F_0}{\partial X_0}(X_0,X_1,X_2) = b_{00}X_0^2 + b_{01}X_1^2 + b_{02}X_2^2 + b_{03}X_0X_1 + b_{04}X_0X_2 + b_{05}X_1X_2$$

  $$\frac{\partial F_1}{\partial X_1}(X_0,X_1,X_2) = b_{10}X_0^2 + b_{11}X_1^2 + b_{12}X_2^2 + b_{13}X_0X_1 + b_{14}X_0X_2 + b_{15}X_1X_2$$

  $$\frac{\partial F_2}{\partial X_2}(X_0,X_1,X_2) = b_{20}X_0^2 + b_{21}X_1^2 + b_{22}X_2^2 + b_{23}X_0X_1 + b_{24}X_0X_2 + b_{25}X_1X_2$$

  
  y hacer ${\bf A} = \left(a_{ij}\right)_{(i,j)\in[\![0,2]\!]\times[\![0,5]\!]}$ , ${\bf B} = \left(b_{ij}\right)_{(i,j)\in[\![0,2]\!]\times[\![0,5]\!]}$ se tendrá:
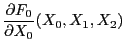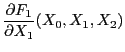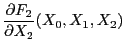  Res$$_{(2,2,2)}(F_0(X_0,X_1,X_2),F_1(X_0,X_1,X_2),F_2(X_0,X_1,X_2)) = -2^{-9}\det\left[\begin{array}{c} {\bf A} \ {\bf B} \end{array}\right]$$

Enlistemos algunas propiedades de los resultantes multipolinomiales. Sean $n\in\mathbb{Z}^+$ , ${\bf d} = (d_0,\ldots,d_n)\in(\mathbb{Z}^+)^{n+1}$ , $I_i= \{{\bf e}\in[\![0,n]\!]\vert \sum_{j=0}^n e_j = d_i\}$ , ${\bf A}_i = \{A_{i,{\bf e}}\vert {\bf e}\in I_i\}$ y ${\bf A} = \bigcup_{ i\in[\![0,n]\!]}{\bf A}_i$ .

Proposición 1.3   Para cada $i\in[\![0,n]\!]$ , el polinomio Res$_{i,d_i}({\bf A}_i) =$   Res$_{{\bf d}}\left({\bf A})\in(\mathbb{Z}[{\bf A}-{\bf A}_i]\right)[{\bf A}_i]$ es homogéneo de grado $\prod_{j\not=i}d_j$ . En consecuencia, el grado total de Res$_{{\bf d}}$ es $\sum_{i=0}^n\prod_{j\not=i}d_j$ .

Para una $(n+1)$ -ada $(\xi_0,\ldots,\xi_i,\ldots,\xi_j,\ldots,\xi_n)$ cualquiera definamos las siguientes operaciones:

• Para una transposición $\tau=(i,j)\in S_{n+1}$ denotemos por
  $$\tau(\xi_0,\ldots,\xi_i,\ldots,\xi_j,\ldots,\xi_n) = (\xi_0,\ldots,\xi_j,\ldots,\xi_i,\ldots,\xi_n)$$
  a la $(n+1)$ -ada que resulta de intercambiar de posición las entradas $i$ y $j$ .
• Para un índice $i$ y un valor $\eta$ denotemos por
  $$\sigma_{i\eta}(\xi_0,\ldots,\xi_i,\ldots,\xi_n) = (\xi_0,\ldots,\eta,\ldots,\xi_n)$$
  a la $(n+1)$ -ada que resulta de remplazar la entrada $i$ -ésima por el valor $\eta$ .

Proposición 1.4   Las siguientes aseveraciones son verdaderas:

• $\forall i,j:\left[i<j \Longrightarrow \mbox{\rm Res}_{{\bf d}}(F_0,\cdots,F_... ... (-1)^{d_0\cdots d_n}\mbox{\rm Res}_{\tau{\bf d}}(\tau(F_0,\cdots,F_n))\right].$
• Si $F_i = F_{i0} F_{i1}$ es el producto de dos polinomios homogéneos de grados respectivos $d_{i0}$ y $d_{i1}$ entonces
  Res$$_{{\bf d}}(F_0,\cdots,F_i,\cdots,F_n) =$$   Res$$_{\sigma_{id_{i0}}({\bf d})}(\sigma_{iF_{i0}}(F_0,\cdots,F_n)\cdot$$Res$$_{\sigma_{id_{i1}}({\bf d})}(\sigma_{iF_{i1}}(F_0,\cdots,F_n).$$

Para un polinomio homogéneo $F({\bf X}_{n+1})\in\mathbb{C}_d[{\bf X}_{n+1}]$ de grado $d$ se define los polinomios:

$$F^{0}({\bf X}_n) = F(\sigma_{n,0}({\bf X}_{n+1})) = F(X_0,\ldots,X_{n-1},0)$$

$$F^{1}({\bf X}_n) = F(\sigma_{n,1}({\bf X}_{n+1})) = F(X_0,\ldots,X_{n-1},1).$$

Es claro que $F^{0}({\bf X}_n)\in\mathbb{C}_d[{\bf X}_n]$ es homogéneo de grado $d$ con una variable menos.

Un análogo a la relación (3) se enuncia como sigue:

Proposición 1.5   Si Res$_{{\bf d}}(F_0,\cdots,F_n) \not= 0$ entonces el cociente $\mathbb{C}[{\bf X}_n]/\left(\left(F_i^{1}({\bf X}_n)\right)_{i=0}^{n-1}\right)$ , visto como un espacio vectorial sobre $\mathbb{C}$ , es de dimensión $d_0\cdots d_{n-1}$ y

Res$$_{{\bf d}}(F_0,\cdots,F_n) = \left(\mbox{\rm Res}_{(d_0,\ldots,d_... ..._n}\hspace{4em}\mbox{({\em F\'ormula de Poisson}\index{F\'ormula de Poisson})},$$

donde $h_{F^{1}_n}:\mathbb{C}[{\bf X}_n]/\left(\left(F_i^{1}({\bf X}_n)\right)_{i=0}^... ... \mathbb{C}[{\bf X}_n]/\left(\left(F_i^{1}({\bf X}_n)\right)_{i=0}^{n-1}\right)$ es la homotecia $[P({\bf X}_n)] \mapsto[F_n^{1}({\bf X}_n) P({\bf X}_n)]$ .