



Siguiente: Ilustración del Teorema de
Un nivel arriba: El teorema de Goodstein
Anterior: Representación formal en base
Para 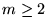 y
y  dados, definiremos a la sucesión de Goodstein
dados, definiremos a la sucesión de Goodstein
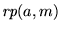 de manera recursiva. Para ello nos auxiliaremos de la sucesión
de manera recursiva. Para ello nos auxiliaremos de la sucesión
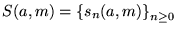 definida igualmente de manera recursiva.
Explícitamente, hacemos
definida igualmente de manera recursiva.
Explícitamente, hacemos
Ejemplo.
Para m=2 y a=100 tenemos
 Luego
Luego
Sorpresivamente tenemos que ... ¡la sucesión de Goodstein converge a cero!
Teorema de Goodstein:

- el teorema se cumple en
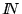 :
el modelo estándar de los números naturales, sin embargo
:
el modelo estándar de los números naturales, sin embargo
- no es demostrable en la aritmética de Peano,
- en términos de (a,m), el mínimo n que anula a la sucesión de Goodstein crece vertiginosamente rápido.
Función de Goodstein: Definimos a la función G como
Puede probarse que la diagonal de G ``domina'' a cualquier función recursiva, es decir:
Se tiene:
- G no puede ser recursiva y
- el Teorema de Goodstein no es demostrable formalmente, pues
- una demostración formal de él daría un algoritmo para calcular G, y no puede existir tal algoritmo pues la función que calcularía tal algoritmo estaría acotada a la larga por G.




Siguiente: Ilustración del Teorema de
Un nivel arriba: El teorema de Goodstein
Anterior: Representación formal en base
Guillermo Morales-Luna
2000-07-10
