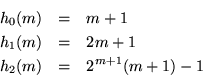


Siguiente: La conjetura de Catalan
Un nivel arriba: El teorema de Goodstein
Anterior: Ilustración del Teorema de
Calcularemos valores para argumentos de la forma
 donde
donde
![$a\in[1,m-1],\;i\in[0,m-1]\mbox{\rm y }m\geq 2.$](img1348.gif) Definamos
Definamos
Entonces
 Recursivamente, para
Recursivamente, para 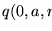 ,
los valores de q y de p se calculan como sigue
,
los valores de q y de p se calculan como sigue
Equivalentemente, se tiene las recurrencias siguientes:
y
De aquí se puede ver que q es ``constante respecto a m'',
 Resolución del sistema de recurrencias
Resolución del sistema de recurrencias
Proposición 4.2
Supongamos que
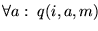
es una función tal que
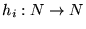
Entonces
- 1.
-
p(i,a,m)=hia(m)-m.
- 2.
-
q(i+1,a,m)=him+1(m)-m.
Demostración: Probemos 1) por inducción en a:
Caso a=1:
Caso a+1:
Sea  .
Supongamos que
p(i,a,m)=hia(m)-m. De acuerdo a la recurrencia localizada para p tenemos
.
Supongamos que
p(i,a,m)=hia(m)-m. De acuerdo a la recurrencia localizada para p tenemos
Probemos ahora 2).
De la recurrencia de q obtenemos
Así pues podemos definir
Ya que
q(0,a,m) = 1 tenemos
h0(m)=m+1.
En resumen, al definir a la sucesión
 haciendo
haciendo
las funciones q y p quedan de la forma
Ejemplos. Tan sólo para ilustrar los crecimientos de las funciones hi observamos:
Para ilustrar el crecimiento de h3 vemos las primeras iteraciones de h2. Se tiene
Pues bien
h3(m)=h2m+1(m).
Los crecimientos de hi con 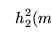 son ciertamente inimaginables.
G(a,m) con a<mm
Hemos visto que si a es de la forma
son ciertamente inimaginables.
G(a,m) con a<mm
Hemos visto que si a es de la forma
 entonces
G(a,m)=p(i,ai,m).
Ahora, si a<mm tenemos que
entonces
G(a,m)=p(i,ai,m).
Ahora, si a<mm tenemos que
![$\exists a_0,\ldots,a_{m-1}\in[0,m-1]$](img1370.gif) tales que
tales que
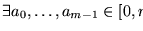 En este caso, G(a,m) es el número de veces que hay que aplicar la construcción de Goodstein para anular a todos los dígitos ai. Teniendo en cuenta que en cada iteración se incrementa la base, vemos que G(a,m) se calcula mediante el algoritmo siguiente:
En este caso, G(a,m) es el número de veces que hay que aplicar la construcción de Goodstein para anular a todos los dígitos ai. Teniendo en cuenta que en cada iteración se incrementa la base, vemos que G(a,m) se calcula mediante el algoritmo siguiente:

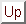


Siguiente: La conjetura de Catalan
Un nivel arriba: El teorema de Goodstein
Anterior: Ilustración del Teorema de
Guillermo Morales-Luna
2000-07-10
 donde
donde

 .
Supongamos que
p(i,a,m)=hia(m)-m. De acuerdo a la recurrencia localizada para p tenemos
.
Supongamos que
p(i,a,m)=hia(m)-m. De acuerdo a la recurrencia localizada para p tenemos

 haciendo
haciendo