



Siguiente: Clases de problemas
Un nivel arriba: Ordenes de funciones
Anterior: Funciones polilogarítmicas
Recordemos aquí la definición de límites inferiores. Sea
 una función real. Entonces
una función real. Entonces
es decir, si para cualquier
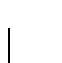 existe
existe
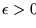 tal que
tal que
Guillermo Morales-Luna
2000-07-10
 una función real. Entonces
una función real. Entonces
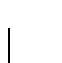 existe
existe