



Siguiente: Tiempos y espacios
Un nivel arriba: Complejidades de tiempo y
Anterior: Complejidades de tiempo y
Consideraremos una clase 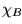 de dispositivos de cómputo, los cuales pueden ser
de dispositivos de cómputo, los cuales pueden ser
- máquinas de Turing,
- programas de alto nivel, digamos ``C'',
- funciones recursivas,
- máquinas RAM,
- etc.
Como cada dispositivo de cómputo es un programa, es decir, es una cadena de longitud finita sobre un alfabeto finito, tenemos que 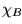 es numerable
es numerable
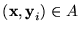 Por otro lado, las entradas posibles a los dispositivos en
Por otro lado, las entradas posibles a los dispositivos en 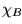 son cadenas de longitud finita sobre un alfabeto de entrada (usualmente Dos={0,1}). Por tanto las entradas también son numerables.
Para un dispositivo M y una entrada
son cadenas de longitud finita sobre un alfabeto de entrada (usualmente Dos={0,1}). Por tanto las entradas también son numerables.
Para un dispositivo M y una entrada
 hacemos
hacemos
Supondremos además que la clase 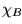 posee un dispositivo universal, es decir, que hay un
posee un dispositivo universal, es decir, que hay un
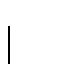 tal que
tal que
donde
 es una codificación de dispositivos en la clase
es una codificación de dispositivos en la clase 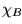 .
Una función
.
Una función
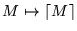 es computable-
es computable-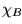 si
si
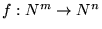
Guillermo Morales-Luna
2000-07-10
 tal que
tal que
 es una codificación de dispositivos en la clase
es una codificación de dispositivos en la clase