



Siguiente: Problemas en teoría de
Un nivel arriba: Problemas con un solo
Anterior: Nociones básicas
Secuenciación en intervalos (Sequencing within intervals):
Instancia:
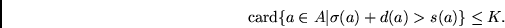
Solución:

Proposición: ``Sequencing within intervals'' es completo-NP.
Demostración: Es evidentemente un problema en NP. Para ver que es difícil-NP, reduzcamos PARTITION a él.
Sea
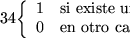 una instancia de PARTITION. Se trata de encontrar
una instancia de PARTITION. Se trata de encontrar
![$J\subset[1,n]$](img1834.gif) tal que
tal que
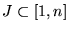 .
Sea
.
Sea
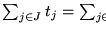 .
Construyamos la siguiente instancia de ``Sequencing within intervals'':
.
Construyamos la siguiente instancia de ``Sequencing within intervals'':
- Por cada sumando tj, definimos,
- una tarea aj, con
- lanzamiento planeado r(aj)=0,
- instante de saturación
s(aj)=B+1, y
- duración
d(aj)=tj.
- Ponemos una tarea ``extra'' a0 con parámetros
Observamos que
Vemos pues que si B es impar entonces ni PARTITION ni ``Sequencing within intervals'' tienen solución.
Ahora, si B es par, toda asignación factible 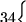 necesariamente hará
necesariamente hará
 ,
y consecuentemente las tareas restantes se dividen en dos conjuntos:
,
y consecuentemente las tareas restantes se dividen en dos conjuntos:
- las que se realizan antes de a0, las cuales disponen, en total, de
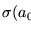 unidades de tiempo para ejecutarse, y
unidades de tiempo para ejecutarse, y
- las que se realizan después de a0, las cuales disponen, en total, también, de
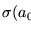 unidades de tiempo para ejecutarse.
unidades de tiempo para ejecutarse.
Tenemos así una solución de PARTITION.
Recíprocamente, de acuerdo con lo anterior, una solución de PARTITION da una asignación factible.
Mínimos retrasos (Minimum tardiness sequencing):
Instancia:
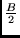
Solución:
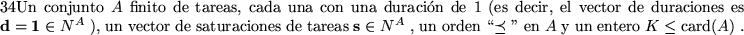
Proposición: ``Minimum tardiness sequencing'' es completo-NP.
Demostración: Para verlo como un problema difícil-NP reduciremos CLIQUE a él.
Sea pues
![$[G=(V,E), J\leq \mbox{\rm card}(V)]$](img1843.gif) una instancia de CLIQUE. Construiremos una instancia de ``Minimum tardiness sequencing'' tal que ésta tendrá una asignación con retrasos acotados por una cota construída si y sólo si la gráfica G contiene a KJ como una subgráfica.
Definamos:
una instancia de CLIQUE. Construiremos una instancia de ``Minimum tardiness sequencing'' tal que ésta tendrá una asignación con retrasos acotados por una cota construída si y sólo si la gráfica G contiene a KJ como una subgráfica.
Definamos:
- Tareas:
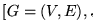 .
.
- Cota:
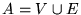 .
.
- Orden de A:
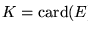
es decir,
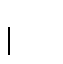 si a es un vértice, b es una arista y a es un vértice extremo de b.
Con esto tendremos que en toda asignación monótona, cada arista ha de ``ejecutarse'' después que cualquiera de sus vértices.
si a es un vértice, b es una arista y a es un vértice extremo de b.
Con esto tendremos que en toda asignación monótona, cada arista ha de ``ejecutarse'' después que cualquiera de sus vértices.
- Saturaciones:
Así pues las únicas tareas que pueden incurrir en retrasos son las correspondientes a las aristas.
Para una asignación 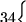 ,
dividamos al conjunto de aristas en dos clases
,
dividamos al conjunto de aristas en dos clases
- las que se realizan a tiempo:
- las que no se realizan a tiempo:
Pues bien, si 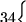 fuese una solución de ``Minimum tardiness sequencing'' entonces
fuese una solución de ``Minimum tardiness sequencing'' entonces
 y consecuentemente
y consecuentemente
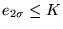 .
Así pues, el entero
.
Así pues, el entero
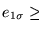 debe estar en el intervalo
debe estar en el intervalo
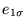 ,
el cual contiene precisamente J enteros.
Si
,
el cual contiene precisamente J enteros.
Si
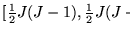 entonces el conjunto de vértices de la gráfica que son extremos de aristas en
entonces el conjunto de vértices de la gráfica que son extremos de aristas en
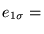 ,
llamémoslo V1, por lo menos tiene J vértices. Esta cota mínima se alcanza cuando
,
llamémoslo V1, por lo menos tiene J vértices. Esta cota mínima se alcanza cuando
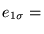 es una gráfica completa KJ.
Por otro lado, como
es una gráfica completa KJ.
Por otro lado, como 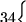 ha de ser monótona, si toda ``tarea'' de
ha de ser monótona, si toda ``tarea'' de
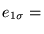 se realiza ``antes'' de
se realiza ``antes'' de
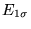 entonces toda ``tarea'' en V1 también ha de realizarse antes de ese tiempo.
Así, se tiene que ambos números
entonces toda ``tarea'' en V1 también ha de realizarse antes de ese tiempo.
Así, se tiene que ambos números
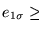 y
y
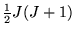 están en el intervalo
están en el intervalo
![$[\frac{1}{2}J(J-1),\frac{1}{2}J(J+1)]$](img1860.gif) .
Esto obliga a que
.
Esto obliga a que
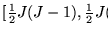 y por tanto los vértices en V1 forman un clan en G con J elementos.
Recíprocamente, si V1 es un conjunto de J vértices que forman un clan en G entonces a ellos y a sus aristas les podemos asociar un ``tiempo'' de ejecución anterior a
y por tanto los vértices en V1 forman un clan en G con J elementos.
Recíprocamente, si V1 es un conjunto de J vértices que forman un clan en G entonces a ellos y a sus aristas les podemos asociar un ``tiempo'' de ejecución anterior a
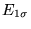 .
La asignación así construída provee una solución de ``Minimum tardiness sequencing''.
.
La asignación así construída provee una solución de ``Minimum tardiness sequencing''.




Siguiente: Problemas en teoría de
Un nivel arriba: Problemas con un solo
Anterior: Nociones básicas
Guillermo Morales-Luna
2000-07-10
 ,
y consecuentemente las tareas restantes se dividen en dos conjuntos:
,
y consecuentemente las tareas restantes se dividen en dos conjuntos:
 si a es un vértice, b es una arista y a es un vértice extremo de b.
Con esto tendremos que en toda asignación monótona, cada arista ha de ``ejecutarse'' después que cualquiera de sus vértices.
si a es un vértice, b es una arista y a es un vértice extremo de b.
Con esto tendremos que en toda asignación monótona, cada arista ha de ``ejecutarse'' después que cualquiera de sus vértices.
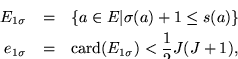
 y consecuentemente
y consecuentemente