


Siguiente: Ecuaciones diofantinas cuadráticas (EDC)
Un nivel arriba: Procedimiento de reducción de
Anterior: Procedimiento de reducción de
Veamos que
1. Si se tiene n variables
 entonces se puede tener
entonces se puede tener
cláusulas de tres literales.
Para cada tal cláusula
y cada asignación
 definimos
definimos
Naturalmente
y
2. Dada una instancia
 de 3SAT, se tiene que una asignación
de 3SAT, se tiene que una asignación
 satisface a
satisface a 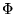 si y sólo si para toda cláusula c de tres literales se tiene
si y sólo si para toda cláusula c de tres literales se tiene
equivalentemente
Si
 es una enumeración de las clásusulas en
es una enumeración de las clásusulas en 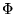 definimos
definimos
RA,i(y)=y - rA(c) + 1.
Por lo anterior,
3. Como
![$\forall A\in\{0,1\}^{[1,m]}, i\leq m, y\in [0,3]:-3\leq R_{A,i}(y)\leq 4$](img1907.gif) tenemos
tenemos
4. Ahora bien, la función
es una biyección.
A cada variable yi la ``parametrizamos'' por dos variables
 haciendo
haciendo
De igual manera, la función
es una biyección.
A cada valor de verdad A(Xi) lo ``parametrizamos'' por una variable
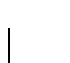 haciendo
haciendo
 sea
sea
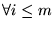 el resultado de sustituir en
RA,i(yi) las parametrizaciones anteriores.
Entonces tenemos
el resultado de sustituir en
RA,i(yi) las parametrizaciones anteriores.
Entonces tenemos
5. Introduzcamos la ecuación
Igualmente se tiene
6. De acuerdo con los parámetros introducidos en la construcción de  se tiene
se tiene
7. Ahora, se tiene el siguiente
Lema: Sean
como en el algoritmo. La solución del problema
es de la forma
8. Así pues, la condición
equivale a que exista una solución x del problema
9. Por otro lado, se tiene el siguiente
Lema: Si p es par y  entonces
entonces
Con esto resulta que el problema
 es equivalente al problema
es equivalente al problema
10. Conjuntando las dos primeras congruencias del problema
 en una sola, vemos que éste equivale al
en una sola, vemos que éste equivale al
11. Finalmente, tomamos
 en
en
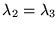 y obtenemos
y obtenemos
lo cual da propiamente  .
.
12. Conversión de soluciones:
![$[\mbox{\it Soluci\'on de }\Phi\Rightarrow\mbox{\it Soluci\'on de }T(\Phi)]$](img1936.gif) :
Dada una asignación que satisfaga a
:
Dada una asignación que satisfaga a 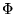 calculamos
calculamos
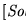 según las ecuaciones en la observación 4. anterior. La solución de
según las ecuaciones en la observación 4. anterior. La solución de  es
es
![$[\mbox{\it Soluci\'on de }T(\Phi)\Rightarrow\mbox{\it Soluci\'on de }\Phi]$](img1939.gif) :
Dada una solución x de
:
Dada una solución x de  localizamos
localizamos
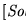 tal que
tal que
y calculamos la asignación que satisface a 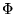 según las ecuaciones en la observación 4. anterior.
(CC) es pues completo-NP.
según las ecuaciones en la observación 4. anterior.
(CC) es pues completo-NP.



Siguiente: Ecuaciones diofantinas cuadráticas (EDC)
Un nivel arriba: Procedimiento de reducción de
Anterior: Procedimiento de reducción de
Guillermo Morales-Luna
2000-07-10
 entonces se puede tener
entonces se puede tener
 definimos
definimos

 de 3SAT, se tiene que una asignación
de 3SAT, se tiene que una asignación
 satisface a
satisface a 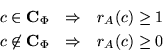
 es una enumeración de las clásusulas en
es una enumeración de las clásusulas en 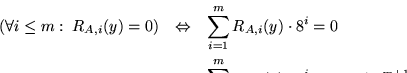
 haciendo
haciendo
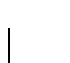 haciendo
haciendo
 sea
sea
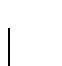 se tiene
se tiene


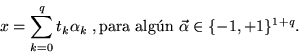
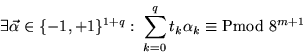
 entonces
entonces
 es equivalente al problema
es equivalente al problema
 en una sola, vemos que éste equivale al
en una sola, vemos que éste equivale al
 en
en
 .
.
 es
es
![$[\mbox{\it Soluci\'on de }T(\Phi)\Rightarrow\mbox{\it Soluci\'on de }\Phi]$](img1939.gif) :
Dada una solución x de
:
Dada una solución x de  localizamos
localizamos