



Siguiente: Divisibilidad simultánea de polinomios
Un nivel arriba: Procedimiento de reducción de
Anterior: Procedimiento de reducción de
Veamos que
1. Dada una instancia
 de 3SAT, se tiene que una asignación
de 3SAT, se tiene que una asignación
 satisface a
satisface a 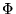 si y sólo si, de acuerdo con la Observación 10. de CC el problema
si y sólo si, de acuerdo con la Observación 10. de CC el problema
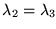 posee una solución.
posee una solución.
2. Tomamos
en
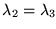 .
Estos valores cumplen con la tercera condición del
.
Estos valores cumplen con la tercera condición del
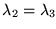 .
La primera ecuación es equivalente a que para algún x2 se tenga
.
La primera ecuación es equivalente a que para algún x2 se tenga
En cuanto a la segunda condición tenemos la equivalencia
Así pues la satisfactibilidad de 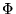 ,
equivalente a la solubildad del
,
equivalente a la solubildad del
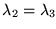 ,
es equivalente a la solubildad en N de la ecuación
,
es equivalente a la solubildad en N de la ecuación
la cual equivale a  .
.
3. Conversión de soluciones:
La conversión de soluciones se hace exactamente igual que en CC.
Guillermo Morales-Luna
2000-07-10
 de 3SAT, se tiene que una asignación
de 3SAT, se tiene que una asignación
 satisface a
satisface a  .
.