Siguiente: Ejemplo: Cadenas equilibradas de Un nivel arriba: Máquinas de Turing Anterior: Máquinas de Turing

Introducción a las máquinas de Turing

Estas son autómatas finitas con dos pilas que tienen un tope común. Ambas pilas forman una cinta. El tope común es la casilla escudriñada (scanned cell), una pila es la parte de la cinta a la derecha de la casilla escudriñada y la otra pila es su parte izquierda. De manera más extensa, podemos plantear a las máquinas de Turing como sigue: Una máquina de Turing M consta

• de una cinta lineal no-acotada conformada por casillas, de hecho la cinta puede ponerse en correspondencia con el conjunto 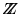$Z\!\!\!Z$ de los números enteros. La única restricción sobre la cinta es que, en todo momento, todas sus casillas están en ``blanco'' salvo un número finito de casillas (aunque ese número finito puede ser arbitrariamente grande),
• de un mecanismo de control que es propiamente un autómata que puede asumir diversos estados,
• de una cabeza lectora que le permite escudriñar, en cada instante, una casilla en la cinta, y
• de un programa, el cual es una lista de quintuplas.

Cada quintupla de M es de la forma $qs\rightarrow ptm$ donde $q,p\in\mbox{\rm Estados}\;,\;s,t\in\mbox{\rm Alfabeto}\;,\;m\in\{\mbox{\rm Izqu},\mbox{\rm Dere},\mbox{\rm Alto}\}$. La connotación que se le asigna a esa quintupla es la siguiente:

``Si en el estado q se lee en la cinta el símbolo s, entonces primero se sustituye a s por t, luego se pasa al estado p y, al final, se pasa a examinar la casilla adyacente en la dirección de m''.

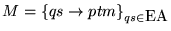Como una primera representación de una máquina M, podemos identificarla con su propio programa. De hecho, al ordenar al conjunto $\mbox{\rm EA}=\mbox{\rm Estados}\times\mbox{\rm Alfabeto},$ la lista de quintuplas $M=\left\{qs\rightarrow ptm\right\}_{qs\in\mbox{\rm EA}}$ puede reescribirse como la lista de ``tercetas'' $M=\left\{ptm\right\}_{qs\in\mbox{\rm EA}}.$

Siguiente: Ejemplo: Cadenas equilibradas de Un nivel arriba: Máquinas de Turing Anterior: Máquinas de Turing