



Siguiente: Ejemplo
Un nivel arriba: Complejidad en redes de
Anterior: Complejidad en redes de
Una red de Petri generalizada, (r.P.g.), es un sistema
R=(L,T,A,p,M) tal que
-
 es una gráfica dirigida, bipartita y ponderada, i. e.:
es una gráfica dirigida, bipartita y ponderada, i. e.:
-
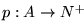 es una función de marcado.
es una función de marcado.
Utilizaremos la terminología siguiente:
-
![$\mbox{\bf m}=\left[M(l_1),\ldots,M(l_n)\right]$](img2048.gif) es el vector de marcado de la r.P.g.
es el vector de marcado de la r.P.g.
- Para cada transición
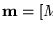 definimos
definimos
- Nociones de entrada de t:
- Nociones de salida de t:
- Una transición
 es disparable si
es disparable si
o, equivalentemente, si
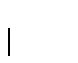 .
.
- Si t es disparable, al dispararse modifica las marcas de sus lugares aledaños:
en otras palabras, cuando t se dispara origina la modificación de marcado en la r.P.g.
- Sea
 un marcado inicial. Una sucesión de disparo es una sucesión de transiciones
un marcado inicial. Una sucesión de disparo es una sucesión de transiciones
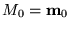 tal que
tal que
- tj1 es disparable con el marcado inicial
 y origina un marcado
y origina un marcado
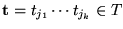 .
.
- Para cada
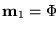 ,
la transición
,
la transición
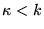 es disparable con el marcado
es disparable con el marcado
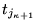 y ha de originar al dispararse al marcado
y ha de originar al dispararse al marcado
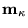
En este caso el marcado
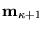 se dice ser el derivado po
se dice ser el derivado po
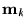 a partir de
a partir de
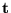 .
Escribamos
.
Escribamos
- Denotamos al conjunto de sucesiones de disparo como
- El conjunto de vectores de marcado que se obtienen por sucesiones de disparo es el conjunto de accesibilidad,
- Dado
 el conjunto de sucesiones de disparo que conducen de
el conjunto de sucesiones de disparo que conducen de
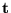 a
a
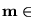 es
es
- Sea
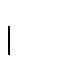 una sucesión de transiciones. La vara de
una sucesión de transiciones. La vara de
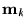 es
es
- Si
 y
y
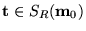 ,
el cambio de marcado es
,
el cambio de marcado es
Denotemos por
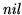 a la palabra vaciía, y por
a la palabra vaciía, y por
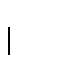 al vector cero.
Es fácil ver que la vara de toda sucesión de disparo se ajusta a las recurrencias
al vector cero.
Es fácil ver que la vara de toda sucesión de disparo se ajusta a las recurrencias
y, correspondientemente, el cambio de marcado satisface
Una r.P.g. R se dice ser
- ordinaria
- si su función de pesos asigna, en cada arista, el valor 1 si existe la arista y 0 en otro caso,
- sin ciclos unitarios
- si para todos
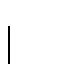 y
y 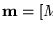 rigen las implicaciones
rigen las implicaciones
- restringida
- si es ordinaria sin ciclos unitarios.
Para una r.P.g. R definiremos los conceptos siguientes:
- marcados accesibles:
-
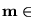 es accesible desde el marcado inicial
es accesible desde el marcado inicial
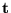 si
si
 .
.
- marcados recubribles:
-
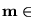 es recubrible desde el marcado inicial
es recubrible desde el marcado inicial
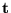 si
si
- lugares acotados:
-
 es un lugar acotado si
es un lugar acotado si
R es acotada para un marcado inicial
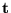 si todos sus lugares se mantienen acotados desde ese marcado.
si todos sus lugares se mantienen acotados desde ese marcado.
- transiciones potencialmente disparables:
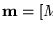 es una transición potencialmente disparable con el marcado
es una transición potencialmente disparable con el marcado
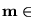 si existe
si existe
 que contiene a t.
que contiene a t.
- marcados muertos-t:
- para una transición t el marcado
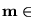 está muerto-t si t no es potencialmente disparable con el marcado
está muerto-t si t no es potencialmente disparable con el marcado
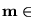 ,
,
- transiciones vivas:
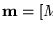 es una transición viva en la r.P.g. R, para el marcado inicial
es una transición viva en la r.P.g. R, para el marcado inicial
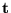 ,
si es potencialmente disparable con todo marcado que sea accesible.
La red misma R está viva con el marcado inicial
,
si es potencialmente disparable con todo marcado que sea accesible.
La red misma R está viva con el marcado inicial
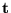 si toda transición está viva para ese marcado inicial.
si toda transición está viva para ese marcado inicial.
- transiciones persistentes:
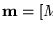 es una transición persistente en la r.P.g. R, para el marcado inicial
es una transición persistente en la r.P.g. R, para el marcado inicial
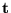 ,
si la única manera de inhabilitarla es mediante su propio disparo. En otras palabras, si se cumple que
,
si la única manera de inhabilitarla es mediante su propio disparo. En otras palabras, si se cumple que
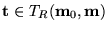 :
:
La red misma R es persistente con el marcado inicial
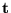 si toda transición es persistente para ese marcado inicial.
si toda transición es persistente para ese marcado inicial.




Siguiente: Ejemplo
Un nivel arriba: Complejidad en redes de
Anterior: Complejidad en redes de
Guillermo Morales-Luna
2000-07-10
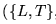 es el conjunto de vértices,
es el conjunto de vértices,
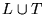 ,
,
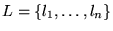 ,
,
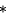
 es una función de pesos o de incidencia.
Un valor nulo de p en una arista es equivalente a la inexistencia de esa arista.
es una función de pesos o de incidencia.
Un valor nulo de p en una arista es equivalente a la inexistencia de esa arista.
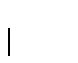 .
.
 un marcado inicial. Una sucesión de disparo es una sucesión de transiciones
un marcado inicial. Una sucesión de disparo es una sucesión de transiciones
 el conjunto de sucesiones de disparo que conducen de
el conjunto de sucesiones de disparo que conducen de
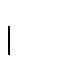 una sucesión de transiciones. La vara de
una sucesión de transiciones. La vara de
 y
y
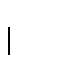 al vector cero.
Es fácil ver que la vara de toda sucesión de disparo se ajusta a las recurrencias
al vector cero.
Es fácil ver que la vara de toda sucesión de disparo se ajusta a las recurrencias
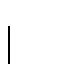 y
y  es un lugar acotado si
es un lugar acotado si
 que contiene a t.
que contiene a t.