



Siguiente: .
Un nivel arriba: Algoritmos probabilísticos
Anterior: Algoritmos probabilísticos
Sea
 un conjunto de m variables. Definimos la clase de expresiones polinomiales enteras
un conjunto de m variables. Definimos la clase de expresiones polinomiales enteras
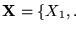 ,
y el grado de cada uno de sus elementos, de manera inductiva como sigue:
,
y el grado de cada uno de sus elementos, de manera inductiva como sigue:
Sea
Consideremos el problema siguiente:
Instancia:

Solución:
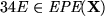
Observaciones: 1. Desarrollando el polinomio dado como una suma de monomios, ordenados lexicográficamente, se resuelve el problema en tiempo exponencial.
2. Si
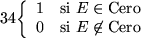 y
y
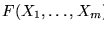 entonces F posee a lo sumo c-1Nm raices enteras en el rectángulo [1,N]m.
entonces F posee a lo sumo c-1Nm raices enteras en el rectángulo [1,N]m.
Guillermo Morales-Luna
2000-07-10
 un conjunto de m variables. Definimos la clase de expresiones polinomiales enteras
un conjunto de m variables. Definimos la clase de expresiones polinomiales enteras