



Siguiente: Máquinas probabilísticas
Un nivel arriba: Algoritmos probabilísticos
Anterior: .
El siguiente algoritmo, debido a Solovay y Strassen, decide probabilísticamente si acaso n es un número primo.
Input:

Output:

Even more
1234567890123456789012345678901234567890 Choose ![$a\in [1,n-1]$](img2148.gif) ;
;
 ;
;
if x>1 then ``No''
else {
 ;
;
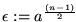 ;
;
if  then ``Yes'' else ``No''
then ``Yes'' else ``No''
}
Observaciones: 1. Igual que antes, al reiterar m veces la selección de números de prueba a la probabilidad de error se minimiza, a lo sumo es 2-m.
2. La complejidad del algoritmo, en cuanto a operaciones aritméticas y cálculos de residuos entre números menores que n2, es
Guillermo Morales-Luna
2000-07-10
;
;
;
;
then ``Yes'' else ``No''