



Siguiente: Máquinas-p
Un nivel arriba: Máquinas probabilísticas
Anterior: Máquinas probabilísticas
Una máquina de Turing probabilística del tipo 1, (mTp1), es una mTnd M modificada de manera que en su árbol de computaciones:
- cada arista tiene un peso numérico
![$p\in [0,1]$](img2154.gif) ,
,
- en cada nodo la suma de los pesos de las aristas que emanan de él es 1,
- el conjunto de nodos terminales es la unión disjunta de nodos de aceptación y de nodos de rechazo,
y
- toda computación es terminal.
Las transiciones en una mTp1 se suponen independientes de sus precedentes, por lo que la probabilidad de una computación es el producto de las probabilidades de las transiciones que la componen.
Alternativamente, en una mTp1 podemos considerar a su función de transición como una de la forma
donde
![$r:Q\times\Sigma\times R\rightarrow [1,n]$](img2157.gif) es una variable aleatoria tal que
es una variable aleatoria tal que
Sea M una mTp1. Para cada cadena de entrada
 sea
sea
El lenguaje reconocido por M es L si y sólo si
Escribiremos L=L(M).
Se tiene evidentemente que
- toda máquina de Turing determinística es una mTp1, en la que en todo instante sólo una transición asume una probabilidad 1, y
- toda mTp1 es una máquina de Turing no-determinística, de hecho las nociones de reconocimiento coinciden, sólo que en una mTp1 se sabe que una cadena reconocida posee al menos
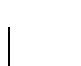 computaciones aceptantes.
computaciones aceptantes.
Consideraremos únicamente mTp1's tales que sus árboles de computación poseen alturas polinomiales en la longitud de sus entradas. Hacemos
Entonces




Siguiente: Máquinas-p
Un nivel arriba: Máquinas probabilísticas
Anterior: Máquinas probabilísticas
Guillermo Morales-Luna
2000-07-10
![$p\in [0,1]$](img2154.gif) ,
,
![$p\in [0,1]$](img2154.gif) ,
,
![$r:Q\times\Sigma\times R\rightarrow [1,n]$](img2157.gif) es una variable aleatoria tal que
es una variable aleatoria tal que
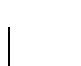 computaciones aceptantes.
computaciones aceptantes.