Siguiente: Algunas inclusiones entre clases Un nivel arriba: Computabilidad con mTp's Anterior: .

.

Así pues, formalmente, la noción de probabilidad no aumenta la capacidad de cómputo. Las ventajas de considerar probabilidades las dan los tiempos y los espacios de cómputo. La función de error en una 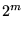$\frac{1}{2}$-mTp M es

$$e_M:x\mapsto\left\{\begin{array}{ll} \mbox{\rm Prob}\{M(x)\... ...row$,} \\ \perp &\mbox{\rm en otro caso.} \end{array}\right.$$

Se tiene que para todo x:

$$x\in\mbox{\rm Dom}(e_M)\;\Rightarrow\;e_M(x)<\frac{1}{2}.$$

Si existe $\epsilon\in]0,\frac{1}{2}[$ tal que

$$x\in\mbox{\rm Dom}(e_M)\;\Rightarrow\;e_M(x)\leq \epsilon,$$

decimos que M calcula a f_M con una probabilidad de error acotada. Resulta claro que una mTdeterminística es una mTp cuya función de error es nula.