



Siguiente: Clase de funciones elementales
Un nivel arriba: Algunos otros esquemas de
Anterior: Esquemas de sumatoria y
En este esquema, dada una función
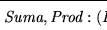 ,
podemos obtener varias funciones, simplemente instanciando algunas variables que aparezcan como argumentos por constantes, o bien por algunas otras variables. Cada posible ``instanciación'' da lugar a una nueva función. Tenemos,
Más precisamente:
Si
,
podemos obtener varias funciones, simplemente instanciando algunas variables que aparezcan como argumentos por constantes, o bien por algunas otras variables. Cada posible ``instanciación'' da lugar a una nueva función. Tenemos,
Más precisamente:
Si
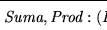 es una función, para
es una función, para 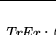 decimos que una función
decimos que una función
 se obtiene por una tranformación explícita a partir de g si es de la forma
se obtiene por una tranformación explícita a partir de g si es de la forma
donde cada  es bien una proyección o una función constante.
es bien una proyección o una función constante.
Guillermo Morales-Luna
2000-07-10

