Siguiente: Codificación con la función Un nivel arriba: Función de Gödel Anterior: Función de Gödel

Definiciones básicas

La función 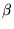$\beta$ de Gödel se define como sigue:

$$\begin{eqnarray*}\beta:I\!\!N^3 &\rightarrow& I\!\!N\\ (x,y,i) &\mapsto& \beta(x,y,i)=x \mbox{\rm mod }{[1+(i+1)y]} \end{eqnarray*}$$

Se ve inmediatamente que valen las propiedades siguientes:

1.

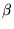$\beta$ es computable.

2.

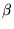$\beta$ es total.

3.

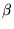$\forall (x,y,i):\ 0\leq \beta(x,y,i)< 1+(i+1)y$. Así pues, $\beta$ tiene un crecimiento a lo sumo cuadrático.

4.

Para cada x,y la función 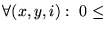$i\mapsto \beta(x,y,i)$ es, a la larga, o sea, a partir de un punto, constante.