



Siguiente: Universalidad
Un nivel arriba: Función de Gödel
Anterior: Codificación con la función
Consideremos la función
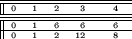 ,
,
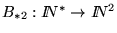 donde
donde
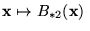 es el vector que se obtiene de anteponer al vector
es el vector que se obtiene de anteponer al vector
 su propia longitud, es decir,
su propia longitud, es decir,
y consideremos también la función
 ,
,
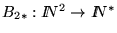 donde
donde
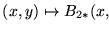 y
y
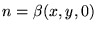 .
El lector se convencerá de inmediato de que se cumplen las relaciones siguientes:
.
El lector se convencerá de inmediato de que se cumplen las relaciones siguientes:
- 1.
- B*2 es inyectiva, es decir:
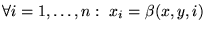 .
.
- 2.
- B*2 no es suprayectiva.
En efecto, de acuerdo con la demostración del teorema 3.3.3, una pareja está en la imagen de
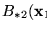 sólo si su ordenada, es decir, su segunda componente, es el factorial de un número.
sólo si su ordenada, es decir, su segunda componente, es el factorial de un número.
- 3.
- B2* no es inyectiva.
En efecto, de las tablas 3.5 y 3.6, vemos que las 14 parejas obtenidas en 3.5 son tales que bajo B2* corresponden a la secuencia vacía, pues ésta es la única de longitud 0.
- 4.
- B2* es suprayectiva, en consecuencia con el teorema 3.3.3.
- 5.
-
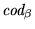 .
.
- 6.
-
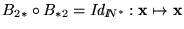 ,
donde
,
donde
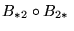 es la imagen, bajo la función
es la imagen, bajo la función
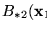 ,
de
,
de 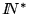 .
.
- 7.
- Si
 es cualquier función de apareamiento (computable) entonces
es cualquier función de apareamiento (computable) entonces
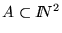 es una enumeración (computable), que no será suprayectiva, del conjunto de secuencias de números naturales.
es una enumeración (computable), que no será suprayectiva, del conjunto de secuencias de números naturales.




Siguiente: Universalidad
Un nivel arriba: Función de Gödel
Anterior: Codificación con la función
Guillermo Morales-Luna
2000-07-10
 ,
,
 es cualquier función de apareamiento (computable) entonces
es cualquier función de apareamiento (computable) entonces