



Siguiente: Teoremas de recursión
Un nivel arriba: Decidibilidad
Anterior: Proyecciones
Para un conjunto
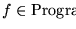 consideremos el problema de decisión siguiente:
consideremos el problema de decisión siguiente:
Problema  :
:
Instancia: Un punto
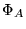 .
.
Respuesta:
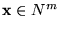
Si A es un conjunto semidecidible el problema anterior es sólo resoluble a medias: Si gA tiene como dominio a A entonces dado el punto
 evaluamos en él a gA. En el caso de que obtengamos un valor, contestamos que el punto pertenece a A pero en caso de no obtenerlo, no podremos saber si la falla en obtener valor alguno es debida a que efectivamente se carece de él o a que aún no concluye gA su proceso de cálculo en
evaluamos en él a gA. En el caso de que obtengamos un valor, contestamos que el punto pertenece a A pero en caso de no obtenerlo, no podremos saber si la falla en obtener valor alguno es debida a que efectivamente se carece de él o a que aún no concluye gA su proceso de cálculo en
 .
El problema de decisión en conjuntos semidecidibles es pues semidecidible.
Para un conjunto decidible, su propia función característica es una algoritmo de solución del problema de decisión correspondiente.
Así pues es altamente deseable contar con un procedimiento para identificar cuándo un programa ha de pararse para una entrada dada. Tal procedimiento es, sin embargo, inexistente.
.
El problema de decisión en conjuntos semidecidibles es pues semidecidible.
Para un conjunto decidible, su propia función característica es una algoritmo de solución del problema de decisión correspondiente.
Así pues es altamente deseable contar con un procedimiento para identificar cuándo un programa ha de pararse para una entrada dada. Tal procedimiento es, sin embargo, inexistente.
Proposición 3.2 (Problema de la Parada)
Existen conjuntos semidecidibles que no son decidibles.
En efecto, sea U un programa universal para la clase de programas. Consideremos el conjunto de parejas correspondientes a programas y entradas en sus dominios de convergencia:
Veamos que
 pero
pero
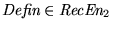 Consideremos el conjunto
Consideremos el conjunto
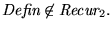 y su complemento
y su complemento
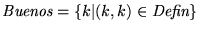 k es pues bueno si k mismo hace converger al k-ésimo programa. En otro caso es malo. Así pues
k es pues bueno si k mismo hace converger al k-ésimo programa. En otro caso es malo. Así pues
Si acaso se tuviera
 entonces ambos conjuntos introducidos serían semidecidibles, es decir,
entonces ambos conjuntos introducidos serían semidecidibles, es decir,
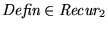 Luego
Luego
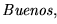 sería el dominio de una función programable, es decir,
sería el dominio de una función programable, es decir,
![$[\exists k_0\forall k: \lfloor k_0\rfloor(\lfloor k\rfloor)\downarrow \;\Leftrightarrow\;k\in \mbox{\it Malos}].$](img899.gif) En particular, para k=k0 tendremos que ha de regir la equivalencia lógica
En particular, para k=k0 tendremos que ha de regir la equivalencia lógica
![$[k_0\in \mbox{\it Buenos}\;\Leftrightarrow\;\lfloor k_0\rfloor(\lfloor k_0\rfloor)\downarrow \Leftrightarrow\;k_0\in \mbox{\it Malos}]$](img900.gif) lo cual es, a todas luces, absurdo.
lo cual es, a todas luces, absurdo.
En conclusión: En cualquier sistema formal de cómputo que se autorrepresente podemos plantear el análogo al problema de la parada. Tal problema no podrá ser resuelto a menos de que el sistema en cuestión sea contradictorio, es decir, que haya un programa que ante una misma entrada terminará con una respuesta 0 o con una respuesta 1 indistintamente.




Siguiente: Teoremas de recursión
Un nivel arriba: Decidibilidad
Anterior: Proyecciones
Guillermo Morales-Luna
2000-07-10
 pero
pero