



Siguiente: Problema de la correspondencia
Un nivel arriba: Irresolubilidad
Anterior: Irresolubilidad
Consideremos la clase de funciones recursivas con un solo argumento. Sea pues
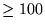 una enumeración efectiva de las funciones computables de una sola variable.
Sea
una enumeración efectiva de las funciones computables de una sola variable.
Sea
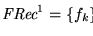 una subclase. El conjunto de índices de
una subclase. El conjunto de índices de 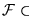 es
es
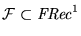 La clase
La clase 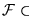 se dice ser recursiva si su conjunto de índices
se dice ser recursiva si su conjunto de índices
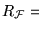 lo es, es decir, si la función característica de este último conjunto es recursiva.
lo es, es decir, si la función característica de este último conjunto es recursiva.
Disgresión: Supongamos que f es una función computable, calculada por el programa P y que el índice de f es k0. Sea
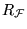 la mónada que consta únicamente de la función f. Tenemos que
la mónada que consta únicamente de la función f. Tenemos que
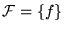 .
Pero la inclusión es estricta, pues f puede ser calculada también por una infinidad de otros programas, es decir, f tiene una infinidad de índices. Para determinar que un número cualquiera k está en
.
Pero la inclusión es estricta, pues f puede ser calculada también por una infinidad de otros programas, es decir, f tiene una infinidad de índices. Para determinar que un número cualquiera k está en
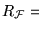 será menester que la función fk coincide con f, la verificación de lo cual es un problema irresoluble, en general, como lo veremos más adelante. La dificultad principal en revisar si acaso una función coincide con otra, estriba en que aún cuando podamos probar uno a uno, y, potencialmente todos, los valores de ambas funciones, ese proceso es interminable pues siempre quedarán más valores pendientes de revisar que los ya revisados.
será menester que la función fk coincide con f, la verificación de lo cual es un problema irresoluble, en general, como lo veremos más adelante. La dificultad principal en revisar si acaso una función coincide con otra, estriba en que aún cuando podamos probar uno a uno, y, potencialmente todos, los valores de ambas funciones, ese proceso es interminable pues siempre quedarán más valores pendientes de revisar que los ya revisados.
Teorema 1.1 (Rice)
Ninguna subclase propia no vacía de funciones recursivas
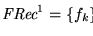
puede ser recursiva.
En otras palabras, si existen
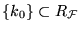
tales que
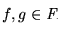
y
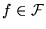
entonces
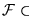
no puede ser recursiva.
Demostración: Supongamos que 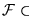 sea recursiva y que existen
sea recursiva y que existen
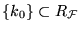 tales que
tales que
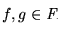 y
y
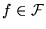 .
Existe pues una función recursiva
.
Existe pues una función recursiva
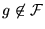 que coincide con la función característica de
que coincide con la función característica de
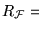 ,
es decir, tal que
,
es decir, tal que
Definamos
 de manera que
de manera que
h es recursiva pues se está definiendo por casos utilizando funciones recursivas. Por el Teorema de Parametrización, existe una función recursiva
 tal que
tal que
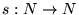 Por el Teorema de Recursión ha de existir un k0 tal que
fk0=fs(k0). Así pues,
Por el Teorema de Recursión ha de existir un k0 tal que
fk0=fs(k0). Así pues,
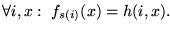 ,
vale decir,
,
vale decir,
Ya que
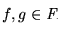 pero
pero
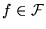 tenemos las equivalencias siguientes:
tenemos las equivalencias siguientes:
y esto es una contradicción.
Digamos que una clase de funciones es trivial si bien es vacía, o bien coincide con toda la clase
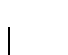 .
El Teorema de Rice asevera pues que las únicas clases de funciones que son recursivas son precisamente las triviales.
.
El Teorema de Rice asevera pues que las únicas clases de funciones que son recursivas son precisamente las triviales.
Corolario 1.1
Las siguientes subclases de
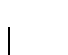
NO son en sí recursivas, es decir, no hay programa alguno para reconocer cuándo una función dada en
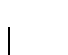
cae en una de esas clases.
El corolario se sigue de inmediato del teorema de Rice pues cada una de las subclases enlistadas es un subconjunto propio no-vacío de
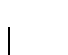 .
.
Teorema 1.2 (Rice: Versión vectorial)
Sea
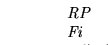
una familia de
m-tuplas cuyas componentes son funciones recursivas. Sea
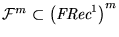
Entonces
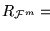
no puede ser recursivo a menos de que
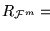
sea trivial, es decir,
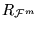
o
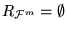
Demostración: Sea
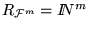 una biyección computable. Dado
una biyección computable. Dado
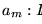 ,
definimos
,
definimos
Se tiene que
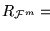 es recursivo si y sólo si S lo es, y S no es trivial si y sólo si
es recursivo si y sólo si S lo es, y S no es trivial si y sólo si
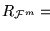 no lo es. Del Teorema de Rice se sigue que S no es recursivo.
no lo es. Del Teorema de Rice se sigue que S no es recursivo.
Corolario 1.2
Las siguientes clases de funciones NO son recursivas.
donde
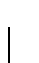
es, por ejemplo, una operación binaria computable.
El corolario se sigue de que las clases enlistadas no son triviales.
Se dice que una función g es una extensión de la función f, o que f es una restricción de g, si se cumple
g extiende propiamente a f si existe x0 tal que
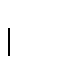 pero
pero
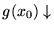 .
.
Teorema 1.3 (Primera extensión del Teorema de Rice)
Sea
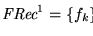
una familia de funciones recursivas tal que existe una función
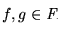
con una extensión propia recursiva
g que NO está en
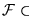
.
Entonces el conjunto de índices
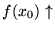
no puede ser recursivamente enumerable.
Demostración: Sean f y g como en el enunciado del teorema. Sea
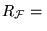 una enumeración efectiva de las funciones recursivas. Consideremos la función
una enumeración efectiva de las funciones recursivas. Consideremos la función
 tal que
tal que
La función
 es claramente computable, pues es la diagonal de una función universal. Sea P un programa que la calcule. Como f y g son recursivas, existen sendos programas Q1,Q2 que las calculan. La función h puede calcularse como sigue:
Dado (i,n),
es claramente computable, pues es la diagonal de una función universal. Sea P un programa que la calcule. Como f y g son recursivas, existen sendos programas Q1,Q2 que las calculan. La función h puede calcularse como sigue:
Dado (i,n),
- 1.
- calculamos P(i) y Q1(x) en ``tiempo compartido'', como si se calculara
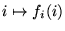 según el procedimiento descrito en 3.4.6,
según el procedimiento descrito en 3.4.6,
- 2.
- si el cálculo de Q1(x) termina primero, se da su valor como salida,
- 3.
- si el cálculo de P(i) termina primero, se pasa a calcular Q2(x) y se da su valor como salida.
Puesto que g es una extensión de f el procedimiento anterior calcula h(i,x). Por tanto, h es recursiva.
Por el Teorema de Parametrización existe una función computable s tal que
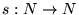 Así pues,
Así pues,
![$\forall i:[s(i)\in R_{{\cal F}}\Leftrightarrow f_i(i)\uparrow]$](img1066.gif) .
Ahora bien, el conjunto
.
Ahora bien, el conjunto
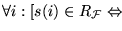 bien que es recursivamente enumerable no es recursivo (éste aparece de manera esencial en el Problema de la Parada). Se tiene además que
bien que es recursivamente enumerable no es recursivo (éste aparece de manera esencial en el Problema de la Parada). Se tiene además que
![$\forall i:[s(i)\in R_{{\cal F}}\Leftrightarrow i\not\in K].$](img1068.gif) Consecuentemente, si
Consecuentemente, si
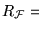 fuera recursivamente enumerable entonces también lo sería el complemento de K y esto obligaría a que K fuera recursivo, lo cual no es posible.
fuera recursivamente enumerable entonces también lo sería el complemento de K y esto obligaría a que K fuera recursivo, lo cual no es posible.
Corolario 1.3
Las siguientes clases de funciones NO son recursivamente enumerables, es decir, no hay programa alguno para generar uno a uno a todos los elementos en una de esas clases.
En efecto, para cada una de esas clases se puede dar un ejemplo particular de una función f en la clase con una extensión fuera de ella.




Siguiente: Problema de la correspondencia
Un nivel arriba: Irresolubilidad
Anterior: Irresolubilidad
Guillermo Morales-Luna
2000-07-10
 de manera que
de manera que
 tal que
tal que
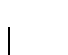 .
El Teorema de Rice asevera pues que las únicas clases de funciones que son recursivas son precisamente las triviales.
.
El Teorema de Rice asevera pues que las únicas clases de funciones que son recursivas son precisamente las triviales.
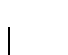 NO son en sí recursivas, es decir, no hay programa alguno para reconocer cuándo una función dada en
NO son en sí recursivas, es decir, no hay programa alguno para reconocer cuándo una función dada en
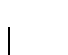 cae en una de esas clases.
cae en una de esas clases.
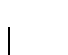 .
.
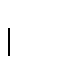 pero
pero
 tal que
tal que
 es claramente computable, pues es la diagonal de una función universal. Sea P un programa que la calcule. Como f y g son recursivas, existen sendos programas Q1,Q2 que las calculan. La función h puede calcularse como sigue:
Dado (i,n),
es claramente computable, pues es la diagonal de una función universal. Sea P un programa que la calcule. Como f y g son recursivas, existen sendos programas Q1,Q2 que las calculan. La función h puede calcularse como sigue:
Dado (i,n),