

Siguiente: Cálculo de predicados difuso
Un nivel arriba: Introducción a la lógica
Anterior: Conjuntos difusos
Recordamos que Gottfried Wilhelm Leibniz2 planteó en el s. XVII la necesidad de un calculus ratiocinator que sería un sistema con un propio formalismo que permitiera la manipulación simbólica de enunciados, en concordancia con las leyes de la lógica, para descubrir nuevas verdades o bien para verificar como verdaderas a tesis postuladas como tales. Por lo menos desde entonces se reconoció la relevancia del manejo (procesamiento) simbólico de enunciados lógicos. Naturalmente, George Boole3 y Gottlob Frege4 contribuyeron de manera notabilísima en el origen mismo del razonamiento automático. Mas, desde la perspectiva de las lógicas difusas, en los antecedentes de ellas es necesario mencionar a Jan 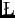 ukasiewicz5. En su sistema trivaluado, si a los valores de verdad Falso, Desconocido y Verdadero se les representa, respectivamente, por los valores numéricos 0,
ukasiewicz5. En su sistema trivaluado, si a los valores de verdad Falso, Desconocido y Verdadero se les representa, respectivamente, por los valores numéricos 0, 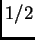 y 1, entonces las nociones de complemento
y 1, entonces las nociones de complemento 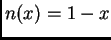 , conjunción
, conjunción
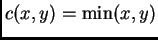 y disyunción
y disyunción
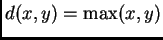 , corresponden a la interpretación intuitiva de esos conectivos lógicos (invitamos al lector a que escriba las tablas de verdad de los conectivos y a que se cerciore de esta aseveración). Este sistema trivaluado entraña, ciertamente, una noción de difusidad.
En un cálculo proposicional difuso se tiene inicialmente una colección de proposiciones primitivas, o ``atómicas'', una serie de conectivos lógicos y reglas definidas de ``buena formación'' de proposiciones ``compuestas'' a partir de las atómicas. Cada proposición puede asumir un valor de verdad que puede ser Falso, o Verdadero o alguno otro ``entre'' esos dos valores extremos de verdad. Cada conectivo lógico tiene asociada una función que determina el valor de verdad de la proposición resultante de él en términos de los valores de verdad de las proposiciones que componen a esa proposición resultante. Resultan entonces sendos problemas ``de deducción'' (dado que los valores de las proposiciones atómicas quedan caracterizados, se ha de caracterizar los de proposiciones compuestas partiendo de ellas) y ``de inferencia'' (dado que los valores de las proposiciones compuestas han sido observados, se ha de formular hipótesis, y además probarlas, respecto a los valores de las proposiciones atómicas involucradas que debieron dar origen a los valores observados). En lo que sigue, detallaremos esta construcción de un cálculo proposicional difuso.
Comencemos con conjuntos de valores de verdad a los cuales llamaremos de valuaciones. Un conjunto de valuación
, corresponden a la interpretación intuitiva de esos conectivos lógicos (invitamos al lector a que escriba las tablas de verdad de los conectivos y a que se cerciore de esta aseveración). Este sistema trivaluado entraña, ciertamente, una noción de difusidad.
En un cálculo proposicional difuso se tiene inicialmente una colección de proposiciones primitivas, o ``atómicas'', una serie de conectivos lógicos y reglas definidas de ``buena formación'' de proposiciones ``compuestas'' a partir de las atómicas. Cada proposición puede asumir un valor de verdad que puede ser Falso, o Verdadero o alguno otro ``entre'' esos dos valores extremos de verdad. Cada conectivo lógico tiene asociada una función que determina el valor de verdad de la proposición resultante de él en términos de los valores de verdad de las proposiciones que componen a esa proposición resultante. Resultan entonces sendos problemas ``de deducción'' (dado que los valores de las proposiciones atómicas quedan caracterizados, se ha de caracterizar los de proposiciones compuestas partiendo de ellas) y ``de inferencia'' (dado que los valores de las proposiciones compuestas han sido observados, se ha de formular hipótesis, y además probarlas, respecto a los valores de las proposiciones atómicas involucradas que debieron dar origen a los valores observados). En lo que sigue, detallaremos esta construcción de un cálculo proposicional difuso.
Comencemos con conjuntos de valores de verdad a los cuales llamaremos de valuaciones. Un conjunto de valuación 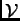 puede ser finito o bien puede ser un contínuo.
Como ejemplos de valuaciones finitas consideremos primero un enfoque de creencias, que a cada proposición atómica le asocia una etiqueta lingüística tal como:
puede ser finito o bien puede ser un contínuo.
Como ejemplos de valuaciones finitas consideremos primero un enfoque de creencias, que a cada proposición atómica le asocia una etiqueta lingüística tal como:
Falso Casi_falso Tal_vez_falso Desconocido Tal_vez_cierto Casi_cierto Verdadero
o bien, con un enfoque de ``posesión de atributos'' del tipo ``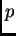 es
es 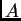 '', las etiquetas lingüísticas pueden ser
'', las etiquetas lingüísticas pueden ser
Definitivamente_no Más_bien_no Al_parecer_no No_se_sabe
Al_parecer_sí Más_bien_sí Definitivamente_sí
De este segundo tipo son las mediciones de variables de control cuando éstas varían de manera discreta, es decir, cuando los aparatos de medición detectan tan solo cambios de una determinada magnitud. El vendedor de telas en la mercería de la esquina mide longitudes con un metro marcado hasta centímetros. Sus ``etiquetas lingüísticas'' serían
.00 .01 .02
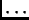
.5
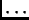
.98 .99 1.
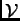 es un conjunto de valuación finito, entonces al enumerar a sus elementos, digamos
es un conjunto de valuación finito, entonces al enumerar a sus elementos, digamos
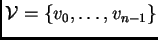 , se puede suponer que esa enumeración concuerda con el orden interno de
, se puede suponer que esa enumeración concuerda con el orden interno de 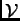 , es decir, si
, es decir, si 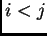 entonces la etiqueta lingüística
entonces la etiqueta lingüística 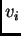 es menor, en el orden de
es menor, en el orden de 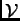 , que
, que 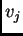 . En tal caso,
. En tal caso, 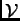 puede identificarse con un subconjunto de números entre 0 y 1, incluyendo éstos, de manera que el primer elemento
puede identificarse con un subconjunto de números entre 0 y 1, incluyendo éstos, de manera que el primer elemento 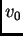 corresponda a 0 y el último,
corresponda a 0 y el último, 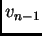 , corresponda a 1 (esto se logra si a cada
, corresponda a 1 (esto se logra si a cada 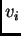 se le asocia el número
se le asocia el número 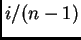 lo cual daría una distribución uniforme de las etiquetas en el intervalo
lo cual daría una distribución uniforme de las etiquetas en el intervalo ![$[0,1]$](img5.png) pero ciertamente ésta no es la única manera de insertar a
pero ciertamente ésta no es la única manera de insertar a 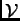 en
en ![$[0,1]$](img5.png) , la manera en la que se inserte dependerá de la aplicación, evidentemente).
Como ejemplos de valuaciones contínuas tenemos los que resultan cuando se estima ``probabilidades de ocurrencia''. Si a una proposición
, la manera en la que se inserte dependerá de la aplicación, evidentemente).
Como ejemplos de valuaciones contínuas tenemos los que resultan cuando se estima ``probabilidades de ocurrencia''. Si a una proposición 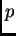 se le asocia la probabilidad de que ocurra (en cierto espacio de eventos) entonces su valor de verdad puede ser un número real entre 0 y 1 inclusive. O bien, cuando se observa una parámetro
se le asocia la probabilidad de que ocurra (en cierto espacio de eventos) entonces su valor de verdad puede ser un número real entre 0 y 1 inclusive. O bien, cuando se observa una parámetro 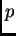 en algún proceso, el cual varía de manera contínua y puede asumir valores entre uno mínimo
en algún proceso, el cual varía de manera contínua y puede asumir valores entre uno mínimo 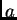 y otro máximo
y otro máximo 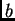 , entonces el propio intervalo
, entonces el propio intervalo ![$[a,b]$](img90.png) constituye un espacio de valuación contínuo.
Utilizando una sencilla regla de tres, es decir, asociándole a cada número
constituye un espacio de valuación contínuo.
Utilizando una sencilla regla de tres, es decir, asociándole a cada número 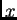 entre
entre 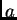 y
y 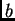 , el número
, el número 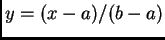 se puede identificar al conjunto de valuación
se puede identificar al conjunto de valuación
![${\cal V}=[a,b]$](img92.png) con el intervalo
con el intervalo ![$[0,1]$](img5.png) .
Así pues, sin ninguna pérdida de generalidad, podremos suponer siempre que el conjunto de valuación
.
Así pues, sin ninguna pérdida de generalidad, podremos suponer siempre que el conjunto de valuación 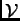 es un subconjunto del intervalo
es un subconjunto del intervalo ![$[0,1]$](img5.png) y contiene a los extremos 0 y 1. Supondremos también que es simétrico respecto al punto medio
y contiene a los extremos 0 y 1. Supondremos también que es simétrico respecto al punto medio 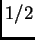 , es decir, supondremos que si para un número
, es decir, supondremos que si para un número 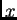 se tiene que
se tiene que 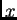 está en
está en 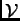 entonces
entonces 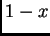 está también en
está también en 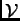 .
Para construir un cálculo proposicional difuso, elijamos un conjunto
.
Para construir un cálculo proposicional difuso, elijamos un conjunto 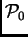 de proposiciones atómicas. Una asignación es una correspondencia que a cada átomo
de proposiciones atómicas. Una asignación es una correspondencia que a cada átomo 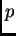 en
en 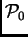 le asocia bien un valor
le asocia bien un valor 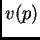 en
en 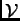 o bien lo deja sin ningún valor asociado.
Supongamos ahora que se tiene tres conectivos lógicos: complemento
o bien lo deja sin ningún valor asociado.
Supongamos ahora que se tiene tres conectivos lógicos: complemento 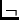 , conjunción
, conjunción 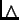 y disyunción
y disyunción 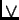 , cada una con una respectiva operación de evaluación, digamos
, cada una con una respectiva operación de evaluación, digamos
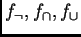 . Entonces la colección de proposiciones booleanas compuestas
. Entonces la colección de proposiciones booleanas compuestas 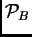 se define como sigue: Todo átomo
se define como sigue: Todo átomo 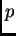 es un elemento de
es un elemento de 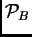 ; el complemento de una proposición en
; el complemento de una proposición en 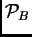 está también en
está también en 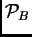 ; y la conjunción y la disyunción de dos proposiciones en
; y la conjunción y la disyunción de dos proposiciones en 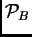 están también en
están también en 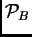 .
Toda asignación
.
Toda asignación 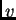 , definida sobre los átomos se extiende naturalmente a una asignación
, definida sobre los átomos se extiende naturalmente a una asignación 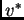 definida en toda la colección
definida en toda la colección 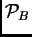 . A saber: Si
. A saber: Si 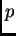 es un átomo, entonces
es un átomo, entonces 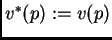 . Si para una proposición
. Si para una proposición 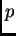 en
en 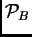 se tiene
se tiene 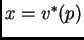 entonces
entonces
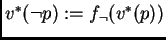 . Similarmente, si para dos proposiciones
. Similarmente, si para dos proposiciones 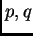 en
en 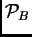 se tiene
se tiene 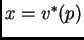 ,
, 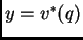 entonces
entonces
En jerga técnica, se dice que la asignación 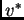 está propagando incertidumbres partiendo de la asignación
está propagando incertidumbres partiendo de la asignación 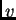 .
Ya hemos visto ejemplos de funciones de evaluación en la sección anterior. En la tabla 1 presentamos un resumen de ellas en el contexto actual y además presentamos una nueva colección de funciones de evaluación debidas también a
.
Ya hemos visto ejemplos de funciones de evaluación en la sección anterior. En la tabla 1 presentamos un resumen de ellas en el contexto actual y además presentamos una nueva colección de funciones de evaluación debidas también a 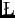 ukasiewicz.
ukasiewicz.
Tabla 1:
Funciones de evaluación para conectivos de complemento, conjunción y disyunción.
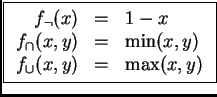 |
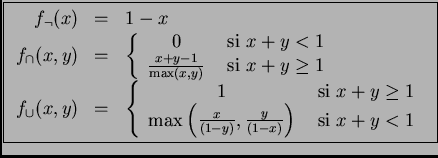 |
| (a) Proporcionalidad |
(b) Creencia
|
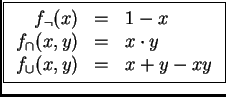 |
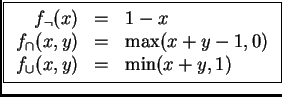 |
| (c) Probabilístico |
(d)  ukasiewicz ukasiewicz |
|
Hasta ahora hemos sólo considerado tres tipos de conectivos lógicos: complemento, conjunción y disyunción. Sin embargo, los demás quedan prácticamente determinados pues siempre se puede definir a la implicación haciendo
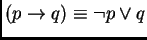 y a la equivalencia lógica haciendo, por ejemplo,
y a la equivalencia lógica haciendo, por ejemplo,
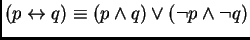 . Recíprocamente, si se tuviese definidas únicamente funciones de evaluación para el complemento y para una implicación ``
. Recíprocamente, si se tuviese definidas únicamente funciones de evaluación para el complemento y para una implicación ``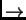 '' entonces se podría definir a los demás conectivos haciendo:
'' entonces se podría definir a los demás conectivos haciendo:
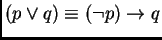 ,
,
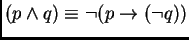 , y
, y
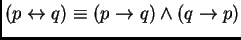 . En varias lógicas difusas se procede según esto último.
Así pues, cada posible selección de funciones de evaluación de conectivos da origen a un distinto cálculo proposicional difuso. Lo que tienen en común todos ellos es que cuando se les restringe a considerar sólo valores de verdad deterministas
. En varias lógicas difusas se procede según esto último.
Así pues, cada posible selección de funciones de evaluación de conectivos da origen a un distinto cálculo proposicional difuso. Lo que tienen en común todos ellos es que cuando se les restringe a considerar sólo valores de verdad deterministas
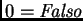 y
y
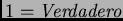 entonces coinciden con el cálculo proposicional clásico. No se puede afirmar que ninguno de los presentados aquí es el correcto. Dependiendo de algunas aplicaciones acaso uno de ellos es el más adecuado, mas dejará de serlo, cuando se cambie de aplicaciones.
entonces coinciden con el cálculo proposicional clásico. No se puede afirmar que ninguno de los presentados aquí es el correcto. Dependiendo de algunas aplicaciones acaso uno de ellos es el más adecuado, mas dejará de serlo, cuando se cambie de aplicaciones.


Siguiente: Cálculo de predicados difuso
Un nivel arriba: Introducción a la lógica
Anterior: Conjuntos difusos
Guillermo Morales-Luna
2002-02-17