

Siguiente: Marcos de referencia
Arriba: Geometría Diferencial y Relatividad
Anterior: Geometría Diferencial y Relatividad
El espacio-tiempo es el espacio real de 4 dimensiones,  . Si
. Si
 , diremos que las tres primeras coordenadas son espaciales y la cuarta
, diremos que las tres primeras coordenadas son espaciales y la cuarta 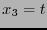 es temporal. Ahí consideramos la forma cuadrática
es temporal. Ahí consideramos la forma cuadrática
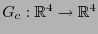 dada por la matriz
dada por la matriz
![\begin{displaymath}
G_c = \mbox{diag}[1\ \ 1\ \ 1\ \ -c^2] = \left(\begin{array}...
...& 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & -c^2
\end{array}\right)
\end{displaymath}](img7.png) |
(1.1) |
con
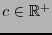 (usualmente
(usualmente  es la velocidad de la luz). Se tiene pues:
es la velocidad de la luz). Se tiene pues:
Ahora bien:
donde
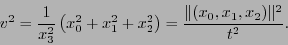 |
(1.2) |
Así el espacio  queda dividido en tres conjuntos:
queda dividido en tres conjuntos:
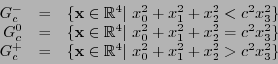 |
(1.3) |
llamadas respectivamente de puntos temporales, lumínicos y espaciales.
Con fines de normalización, consideremos 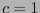 y
y 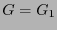 . La pareja
. La pareja
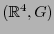 se dice ser el espacio de Minkowski.
Sea
se dice ser el espacio de Minkowski.
Sea
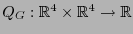 ,
,
 .
.
Para un punto
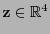 , la traslación
, la traslación
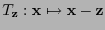 , es tal que
, es tal que
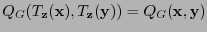 , es decir, es una isometría. Para una transformación lineal
, es decir, es una isometría. Para una transformación lineal
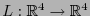 se tendrá
se tendrá
Sea
 . Claramente,
. Claramente, 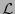 es un subgrupo del grupo multiplicativo
es un subgrupo del grupo multiplicativo
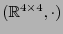 de matrices de orden
de matrices de orden 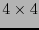 , y se llama grupo de transformaciones de Lorentz. Al escribir una matriz
, y se llama grupo de transformaciones de Lorentz. Al escribir una matriz
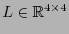 como
como
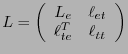 , se tiene
, se tiene
por tanto 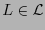 si y sólo si se cumplen las condiciones siguientes:
si y sólo si se cumplen las condiciones siguientes:
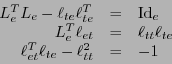 |
(1.4) |
En particular, valen las relaciones (1.4) si
![$\ell_{et} = \ell_{et} = [0\ \ 0\ \ 0]^T$](img33.png) ,
, 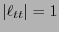 y
y
 es una matriz unitaria de orden
es una matriz unitaria de orden 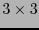 . Tenemos así que el grupo
. Tenemos así que el grupo  se identifica con un subgrupo del grupo de Lorentz mediante el monomorfismo
se identifica con un subgrupo del grupo de Lorentz mediante el monomorfismo
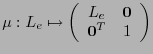 .
Si se considera el grupo especial
.
Si se considera el grupo especial 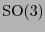 que consta de las transformaciones unitarias que preservan orientación, es decir aquellas con determinante 1, su imagen
que consta de las transformaciones unitarias que preservan orientación, es decir aquellas con determinante 1, su imagen
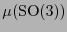 es el grupo especial de Lorentz. De hecho, es usual escribir
es el grupo especial de Lorentz. De hecho, es usual escribir
 y
y
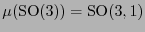 .
.
Por ejemplo, una rotación
con
![$s\in[-\pi,\pi]$](img44.png) , es un elemento de
, es un elemento de
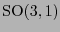 .
.
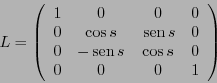
Como otro ejemplo, una rotación espacio-temporal (llamada en inglés boost (empujón)) es de la forma
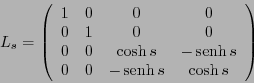 |
(1.5) |
con
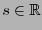 . La transformación
. La transformación 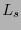 satisface las relaciones (1.4), por lo que está en el grupo de Lorentz. Dado un sistema de referencia con coordenadas
satisface las relaciones (1.4), por lo que está en el grupo de Lorentz. Dado un sistema de referencia con coordenadas
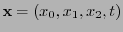 , sea
, sea
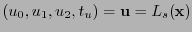 el vector de coordenadas de un nuevo sistema al aplicar
el vector de coordenadas de un nuevo sistema al aplicar 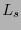 .
Se tiene que cuando
.
Se tiene que cuando  , se ha de tener
, se ha de tener
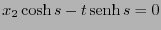 , o sea
, o sea
de donde, en general se tendrá
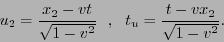 |
(1.6) |
Las relaciones (1.6) determinan el estrechamiento de la distancia y la dilatación del tiempo. El eje 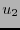 (en el espacio imagen) es
(en el espacio imagen) es
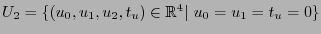 y el eje
y el eje 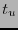 es
es
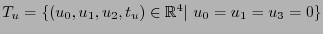 . Sus imágenes inversas bajo la rotación espacio-temporal son respectivamente
. Sus imágenes inversas bajo la rotación espacio-temporal son respectivamente
de donde se ve que ``tiempo'' y ``distancia'' en el marco ``x'' se intercambian en el marco ``u''. Ahora bien
así que al ``acercarse a la velocidad de la luz'', 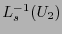 y
y  tienden a las rectas
tienden a las rectas  , similarmente, en el marco ``u'',
, similarmente, en el marco ``u'', 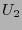 y
y 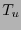 tienden a las rectas
tienden a las rectas  .
.



Siguiente: Marcos de referencia
Arriba: Geometría Diferencial y Relatividad
Anterior: Geometría Diferencial y Relatividad
Guillermo M. Luna
2011-01-03
![]() . Si
. Si
![]() , diremos que las tres primeras coordenadas son espaciales y la cuarta
, diremos que las tres primeras coordenadas son espaciales y la cuarta ![]() es temporal. Ahí consideramos la forma cuadrática
es temporal. Ahí consideramos la forma cuadrática
![]() dada por la matriz
dada por la matriz
![]() y
y ![]() . La pareja
. La pareja
![]() se dice ser el espacio de Minkowski.
Sea
se dice ser el espacio de Minkowski.
Sea
![]() ,
,
![]() .
.
![]() , la traslación
, la traslación
![]() , es tal que
, es tal que
![]() , es decir, es una isometría. Para una transformación lineal
, es decir, es una isometría. Para una transformación lineal
![]() se tendrá
se tendrá
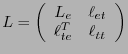 , se tiene
, se tiene
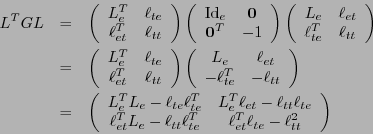
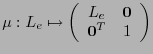 .
Si se considera el grupo especial
.
Si se considera el grupo especial