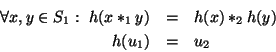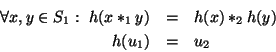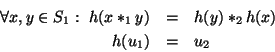


Siguiente: Relaciones de equivalencia congruentes
Un nivel arriba: Monoide de cadenas
Anterior: Orden lexicográfico
Sean
(S1,*1,u1) y
(S2,*2,u2) dos monoides con operaciones respectivas *1 y *2 y unidades u1 y u2. Una función
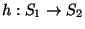 es un homomorfismo si
es un homomorfismo si
En otras palabras, un homomorfismo es una correspondencia entre monoides que preserva las operaciones.
Observación 2.1
El tomar
longitudes da un homomorfismo
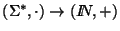
:
En efecto, sea
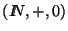 el monoide que consta de los números naturales con la suma como operación y el 0 como unidad. Sea
el monoide que consta de los números naturales con la suma como operación y el 0 como unidad. Sea  un alfabeto. Ya que
un alfabeto. Ya que
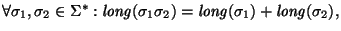 y además
y además
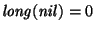 tenemos que
tenemos que
 es un homomorfismo.
es un homomorfismo.
Ejemplos de homomorfismos.
1. Sea
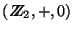 el monoide sobre el conjunto
el monoide sobre el conjunto
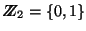 con la operación suma ''módulo 2'', o, en otras palabras, el complemento de la disyunción exclusiva, XOR. Sea
con la operación suma ''módulo 2'', o, en otras palabras, el complemento de la disyunción exclusiva, XOR. Sea  un alfabeto y
un alfabeto y
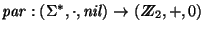 la función definida como
la función definida como
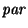 es, en efecto, un homomorfismo.
es, en efecto, un homomorfismo.
2. Sea  un alfabeto y sea
un alfabeto y sea
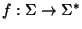 cualquier función. Extendemos f a una función
cualquier función. Extendemos f a una función
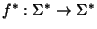 haciendo
haciendo
f* es un homomorfismo y es, propiamente, una sustitución de símbolos: en cada palabra, cada símbolo s se sustituye por la partícula f(s). El homomorfismo f* se dice libre de
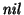 si para ningún
si para ningún
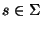 se tiene
se tiene
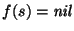 .
.
3. Sea  un alfabeto. Dadas dos palabras
un alfabeto. Dadas dos palabras
 diremos que
diremos que
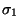 es un prefijo de
es un prefijo de 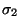 si
si

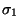 es un sufijo de
es un sufijo de 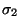 si
si

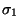 es un enfijo de
es un enfijo de 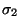 si
si
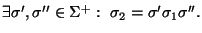
Sea n>0. Consideremos la operación
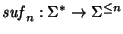 que actúa sobre cualquier palabra suprimiendo, si fuera necesario, un prefijo para quedarse únicamente con el sufijo de longitud n. Más precisamente,
que actúa sobre cualquier palabra suprimiendo, si fuera necesario, un prefijo para quedarse únicamente con el sufijo de longitud n. Más precisamente,
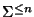 tiene una estructura de monoide con la operación de concatenación, seguida de
tiene una estructura de monoide con la operación de concatenación, seguida de
 ,
,
Bajo esta transformación que es, en efecto, un homomorfismo, todas las palabras de longitud a lo sumo n permanecen fijas.
Sea
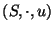 un monoide cualquiera. Consideremos el monoide aditivo sobre el conjunto de números naturales con la suma usual,
un monoide cualquiera. Consideremos el monoide aditivo sobre el conjunto de números naturales con la suma usual,
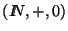 .
Entonces se tiene que para todo
.
Entonces se tiene que para todo 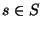 existe un único homomorfismo
existe un único homomorfismo
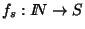 tal que fs(1)=s.
La imagen de tal homomorfismo es el submonoide
tal que fs(1)=s.
La imagen de tal homomorfismo es el submonoide
 y se dice ser el generado por el elemento
y se dice ser el generado por el elemento 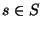 .
.
Un antihomomorfismo entre dos monoides
(S1,*1,u1) y
(S2,*2,u2) es una función
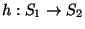 tal que
tal que
es decir, es una operación que en el contradominio ''conmuta'' a la operación.
Ejemplos.
1. Si S2 es conmutativo, entonces cualquier homomorfismo es también un antihomomorfismo.
2. Sea  un alfabeto y sea
un alfabeto y sea
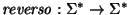 la función que intercambia de derecha a izquierda los símbolos que conforman una palabra. Inductivamente, se tiene
la función que intercambia de derecha a izquierda los símbolos que conforman una palabra. Inductivamente, se tiene
Se ve fácilmente que
y consecuentemente esta función es un antihomomorfismo.
Las palabras fijas bajo este operador son palíndromas.
Como meros ejemplos, se tiene a los siguientes:



Siguiente: Relaciones de equivalencia congruentes
Un nivel arriba: Monoide de cadenas
Anterior: Orden lexicográfico
Guillermo Morales-Luna
2000-06-27