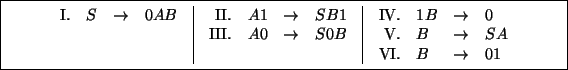Siguiente: Autómatas finitos y expresiones
Un nivel arriba: Gramáticas formales
Anterior: Ejercicios
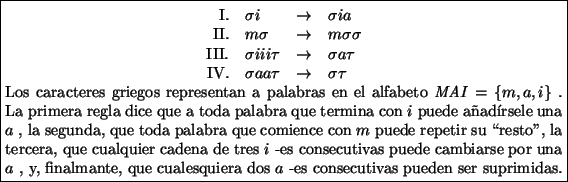
1. Considere la regla de transformación MAI visto en la sección 1.2.1:
Si
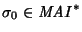 ,
el árbol de derivación de
,
el árbol de derivación de 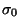 es el árbol (tal vez infinito, pero tal que cada nodo posee un conjunto finito de hijos)
es el árbol (tal vez infinito, pero tal que cada nodo posee un conjunto finito de hijos)
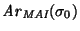 cuyos nodos están etiquetados por palabras en
cuyos nodos están etiquetados por palabras en
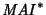 y cuyas aristas lo están por las producciones I, II., III. o IV. definido recursivamente como sigue:
y cuyas aristas lo están por las producciones I, II., III. o IV. definido recursivamente como sigue:
- 1.
- La raíz de
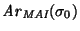 tiene como etiqueta a
tiene como etiqueta a 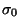 .
.
- 2.
- Para cada nodo de
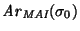 ,
digamos que etiquetado con la palabra
,
digamos que etiquetado con la palabra  ,
si no se le puede aplicar ninguna producción a
,
si no se le puede aplicar ninguna producción a  entonces este nodo se declara como hoja, en otro caso,
entonces este nodo se declara como hoja, en otro caso,
- (a)
- pongamos un contador de hijos h igual a 0, y apliquemos, en tanto sea posible, las reglas siguientes en el orden en que las presentamos:
- (b)
- si
 termina con i,
termina con i,
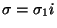 ,
hacemos h:=h+1 y le añadimos un h-ésimo hijo a
,
hacemos h:=h+1 y le añadimos un h-ésimo hijo a  etiquetándolo con
etiquetándolo con
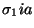 ,
y a la arista que los une con I.,
,
y a la arista que los une con I.,
- (c)
- si
 comienza con m,
comienza con m,
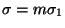 ,
hacemos h:=h+1 y le añadimos un h-ésimo hijo a
,
hacemos h:=h+1 y le añadimos un h-ésimo hijo a  etiquetándolo con
etiquetándolo con
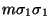 ,
y a la arista que los une con II.,
,
y a la arista que los une con II.,
- (d)
- si
 contiene la cadena iii, para cada vez que aparezca esa cadena, es decir siempre que podamos escribir
contiene la cadena iii, para cada vez que aparezca esa cadena, es decir siempre que podamos escribir
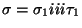 ,
hacemos h:=h+1 y le añadimos un h-ésimo hijo a
,
hacemos h:=h+1 y le añadimos un h-ésimo hijo a  etiquetándolo con
etiquetándolo con
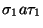 ,
y a la arista que los une con III.,
,
y a la arista que los une con III.,
- (e)
- si
 contiene la cadena aa, para cada vez que aparezca esa cadena, es decir siempre que podamos escribir
contiene la cadena aa, para cada vez que aparezca esa cadena, es decir siempre que podamos escribir
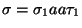 ,
hacemos h:=h+1 y le añadimos un h-ésimo hijo a
,
hacemos h:=h+1 y le añadimos un h-ésimo hijo a  etiquetándolo con
etiquetándolo con
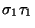 ,
y a la arista que los une con IV.
,
y a la arista que los une con IV.
Escriba un programa que reciba una cadena
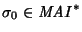 y un número natural n y enliste los n primeros nodos de
y un número natural n y enliste los n primeros nodos de
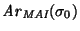 en un recorrido ``a lo ancho'' (si no los hubiere ha de indicar que éste es el caso).
en un recorrido ``a lo ancho'' (si no los hubiere ha de indicar que éste es el caso).
2. Considere la gramática del recuadro siguiente:
El árbol de derivación de S es el árbol (tal vez infinito, pero tal que cada nodo posee un conjunto finito de hijos)
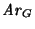 cuyos nodos están etiquetados por palabras en
(S+A+B+0+1)* y cuyas aristas lo están por las producciones I, II., III., IV., V., VI. definido recursivamente como sigue:
cuyos nodos están etiquetados por palabras en
(S+A+B+0+1)* y cuyas aristas lo están por las producciones I, II., III., IV., V., VI. definido recursivamente como sigue:
- 1.
- La raíz de
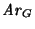 tiene como etiqueta a S.
tiene como etiqueta a S.
- 2.
- Para cada nodo de
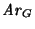 ,
digamos que etiquetado con la palabra
,
digamos que etiquetado con la palabra  ,
si
,
si
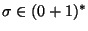 entonces este nodo se declara como hoja, en otro caso, se aplica la producción que corresponda, examinando
entonces este nodo se declara como hoja, en otro caso, se aplica la producción que corresponda, examinando  por la izquierda y las producciones en el orden enlistado.
por la izquierda y las producciones en el orden enlistado.
Escriba un programa que partiendo del símbolo inicial S y un número natural n, enliste los n primeros nodos de
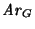 en un recorrido ``a lo ancho'' (si no los hubiere ha de indicar que éste es el caso). Decida si el lenguaje de esta gramática es o no vacío.
en un recorrido ``a lo ancho'' (si no los hubiere ha de indicar que éste es el caso). Decida si el lenguaje de esta gramática es o no vacío.
3. Siguiendo la idea del algoritmo de Markov mostrado en la sección 1.2.3, diseñe un algoritmo de Markov para multiplicar por el entero 5 números enteros en binario. Escriba un programa que reciba como entrada la representación en base 2 de un entero n y muestre visualmente la aplicación sobre él del algoritmo que lo ``quintuplica''.
4. Enumeración con representación en octetos: Utilice la representación en base 256=28 de los números enteros. Cada dígito en tal representación es un byte. Un arreglo de k bytes
![$\mbox{\bf a}=[a_{k-1},a_{k-2},\ldots,a_{1},a_{0}]$](img558.gif) ,
,
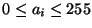 representa al número
representa al número
Imprima a cada dígito ai como una pareja de dígitos hexadecimales:
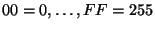 Para un alfabeto
Para un alfabeto 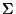 de m caracteres considere la enumeración
de m caracteres considere la enumeración
 definida en la Proposición 2.2.4.
Escriba sendos programas para los problemas siguientes:
definida en la Proposición 2.2.4.
Escriba sendos programas para los problemas siguientes:
- 1.
- Dada m y una cadena
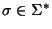 ,
calcule
,
calcule 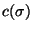 y lo exprese representado en octetos.
y lo exprese representado en octetos.
- 2.
- Dada m y un número entero x representado en octetos, calcule
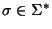 tal que
tal que
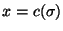 .
.
5. Sea
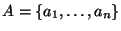 un conjunto de n elementos. Para cada relación binaria
un conjunto de n elementos. Para cada relación binaria
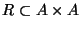 ,
consideremos la matriz
,
consideremos la matriz
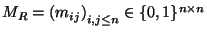 ,
llamada de adyacencia, tal que
,
llamada de adyacencia, tal que
Escriba un programa que dados
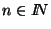 y una matriz
y una matriz
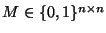 decida (de manera efectiva y eficiente) si la relación R cuya matriz de adyacencia es M es:
decida (de manera efectiva y eficiente) si la relación R cuya matriz de adyacencia es M es:
- 1.
- reflexiva,
- 2.
- simétrica,
- 3.
- antisimétrica,
- 4.
- transitiva,
- 5.
- de equivalencia,
- 6.
- de orden.
De la evidencia que dé este programa, conjeture cuántas relaciones que sean a la vez reflexivas, simétricas, antisimétricas y transitivas puede haber en un conjunto de n elementos. Demuestre que su conjetura es correcta.
6. Experimento de conteo a la Monte Carlo de relaciones de equivalencia: Escriba un programa que dado n, genere de manera aleatoria una relación que sea a la vez reflexiva y simétrica.
Escriba un programa que dados n y k, realice k veces el experimento siguiente: Genera de manera aleatoria una relación que sea a la vez reflexiva y simétrica. Si ésta fuese también transitiva incrementa un contador. Luego de las k repeticiones, el programa ha de calcular la razón del contador entre k.
¿A cuáles valores, en función de n, esperaría usted que converjan esas razones, cuando k se incrementa arbitrariamente?
Pruebe este programa para valores de n entre 20 y 100 y de k no menor que 105.
7. Experimento de conteo a la Monte Carlo de relaciones de orden: Escriba un programa que dado n, genere de manera aleatoria una relación que sea a la vez reflexiva y antisimétrica.
Escriba un programa que dados n y k, realice k veces el experimento siguiente: Genera de manera aleatoria una relación que sea a la vez reflexiva y antisimétrica. Si ésta fuese también transitiva incrementa un contador. Luego de las k repeticiones, el programa ha de calcular la razón del contador entre k.
¿A cuáles valores, en función de n, esperaría usted que converjan esas razones, cuando k se incrementa arbitrariamente?
Pruebe este programa para valores de n entre 20 y 100 y de k no menor que 105.
8. Escriba un programa que dado n, genere de manera aleatoria una relación de equivalencia en un conjunto A de n elementos. Para cada tal relación R, describa al cociente A/R y calcule el índice de R.
Repita este experimento y grafique una tabla de frecuencias considerando los índices.
9. Escriba un programa que dado n, genere de manera aleatoria una relación de orden en un conjunto A de n elementos. Para cada tal relación R, dibuje a su gráfica dirigida G(A,R): los nodos son los elementos de A y entre dos nodos x,y, 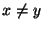 ,
habrá una arista de x a y si xRy y no hay un tercer elemento z tal que xRz y zRy.
,
habrá una arista de x a y si xRy y no hay un tercer elemento z tal que xRz y zRy.
10. Sea 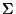 un alfabeto. Considere la relación de orden:
un alfabeto. Considere la relación de orden:
- Prefijo:
- Una palabra es menor que otra si es un prefijo de ella.
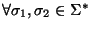 :
:
Escriba programas para resolver cada uno de los problemas siguientes:
- 1.
- Dadas dos palabras
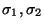 decida si acaso una es menor que la otra.
decida si acaso una es menor que la otra.
- 2.
- Para un conjunto dado de palabras
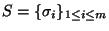 calcule la matriz de orden
calcule la matriz de orden
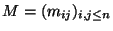 :
:
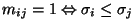 .
Una cadena es un subconjunto ordenado linealmente, es decir, cualesquiera dos elementos de ella se comparan entre sí. La cadena es maximal si no está contenida propiamente en ninguna otra.
En este caso encuentre todas las cadenas maximales posibles.
.
Una cadena es un subconjunto ordenado linealmente, es decir, cualesquiera dos elementos de ella se comparan entre sí. La cadena es maximal si no está contenida propiamente en ninguna otra.
En este caso encuentre todas las cadenas maximales posibles.
11. Sea 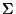 un alfabeto. Considere la relación de orden:
un alfabeto. Considere la relación de orden:
- Monotonía:
- Una palabra es menor que otra si todos sus símbolos aparecen, en el mismo orden, en ella.
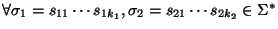 :
:
Escriba programas para resolver cada uno de los problemas siguientes:
- 1.
- Dadas dos palabras
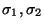 decida si acaso una es menor que la otra.
decida si acaso una es menor que la otra.
- 2.
- Para un conjunto dado de palabras
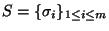 calcule la matriz de orden
calcule la matriz de orden
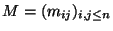 :
:
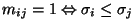 .
Encuentre todas las cadenas maximales posibles.
.
Encuentre todas las cadenas maximales posibles.
12. Sea
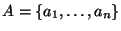 un conjunto de n elementos. Para cada operación binaria
un conjunto de n elementos. Para cada operación binaria
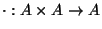 ,
consideremos su tabla de multiplicación
,
consideremos su tabla de multiplicación
![$M=\left(m_{ij}\right)_{i,j\leq n}\in [\![1,n]\!]^{n\times n}$](img581.gif) ,
tal que
,
tal que
Escriba un programa que dados
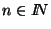 y una matriz
y una matriz
![$M\in [\![1,n]\!]^{n\times n}$](img583.gif) decida (de manera efectiva y eficiente) si la operación cuya tabla de multiplicación es M es:
decida (de manera efectiva y eficiente) si la operación cuya tabla de multiplicación es M es:
- 1.
- conmutativa,
- 2.
- posee una unidad derecha,
- 3.
- posee una unidad izquierda,
- 4.
- asociativa,
- 5.
- dado que existe una unidad, decidir si cada elemento posee un inverso,
- 6.
- un monoide,
- 7.
- un grupo.
13. Consideraremos conjuntos
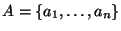 de n elementos con una operación binaria
de n elementos con una operación binaria
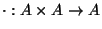 ,
dada por su tabla de multiplicación
,
dada por su tabla de multiplicación
![$M=\left(m_{ij}\right)_{i,j\leq n}\in [\![1,n]\!]^{n\times n}$](img581.gif) en los que se define una relación de equivalencia mediante su matriz de adyacencia,
en los que se define una relación de equivalencia mediante su matriz de adyacencia,
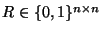 .
Escriba un programa que dados
.
Escriba un programa que dados
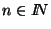 ,
una tabla de multiplicación
,
una tabla de multiplicación
![$M\in [\![1,n]\!]^{n\times n}$](img583.gif) y una equivalencia
y una equivalencia
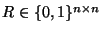 decida (de manera efectiva y eficiente) si la equivalencia es congruente con la multiplicación. En tal caso, calcule la tabla de multiplicación del cociente A/R.
Sugerencia: Ejemplifique considerando dos números primos p, q. Haga
decida (de manera efectiva y eficiente) si la equivalencia es congruente con la multiplicación. En tal caso, calcule la tabla de multiplicación del cociente A/R.
Sugerencia: Ejemplifique considerando dos números primos p, q. Haga
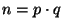 .
Considere la operación
.
Considere la operación
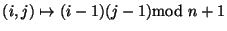 y la relación
y la relación
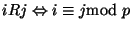 .
Ejemplifique también considerando la tabla de mutiplicación del grupo de permutaciones Sk, con k! elementos. Considere como relación
.
Ejemplifique también considerando la tabla de mutiplicación del grupo de permutaciones Sk, con k! elementos. Considere como relación
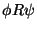 si y sólo si la composición
si y sólo si la composición
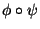 es una permutación par. (Revise un libro de Algebra Moderna, si fuera necesario, para aclarar la terminología que uso.)
es una permutación par. (Revise un libro de Algebra Moderna, si fuera necesario, para aclarar la terminología que uso.)
14. Producto de monoides: Dados dos monoides
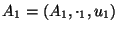 y
y
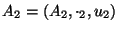 el monomio producto de ellos dos es
el monomio producto de ellos dos es
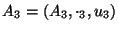 ,
donde
,
donde
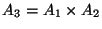 ,
la operación está definida ``componente-a-componente''
,
la operación está definida ``componente-a-componente''
y
u3=(u1,u2). Si n1 es el número de elementos en A1 y n2 el de A2 entonces su producto tendrá
n3=n1n2 elementos. Enumeremos a los elementos de A3 como
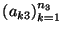 ,
donde
,
donde
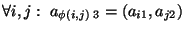 ,
y
,
y
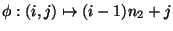 .
Escriba un programa que dados dos monoides A1, A2 con sendas tablas de multiplicación
.
Escriba un programa que dados dos monoides A1, A2 con sendas tablas de multiplicación
![$M_1\in [\![1,n_1]\!]^{n_1\times n_1}$](img598.gif) ,
,
![$M_2\in [\![1,n_2]\!]^{n_2\times n_2}$](img599.gif) ,
escriba la tabla de multiplicación del producto A3, de acuerdo con la enumeración
,
escriba la tabla de multiplicación del producto A3, de acuerdo con la enumeración 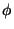 .
.
15. Homomorfismo de monoides: Escriba un programa que dados dos monoides A1, A2 con sendas tablas de multiplicación
![$M_1\in [\![1,n_1]\!]^{n_1\times n_1}$](img598.gif) ,
,
![$M_2\in [\![1,n_2]\!]^{n_2\times n_2}$](img599.gif) ,
decida si existe o no un homomorfismo
,
decida si existe o no un homomorfismo
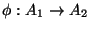 .
En caso de que exista, localice un homomorfismo, y de hecho a todos los posibles homomorfismos.
.
En caso de que exista, localice un homomorfismo, y de hecho a todos los posibles homomorfismos.
16. Sea Zm el anillo de enteros módulo m. Sea
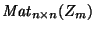 el conjunto de matrices
el conjunto de matrices 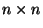 con entradas en Zm. Con la multiplicación de matrices,
con entradas en Zm. Con la multiplicación de matrices,
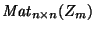 forma un monoide. Si
forma un monoide. Si
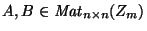 son dos matrices, cualquier palabra
son dos matrices, cualquier palabra
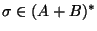 determina una matriz en
determina una matriz en
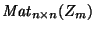 ,
a saber, la que se obtiene al interpretar la conjunción de dos símbolos como el producto de matrices. Introduzcamos la relación de equivalencia en (A+B)* siguiente:
,
a saber, la que se obtiene al interpretar la conjunción de dos símbolos como el producto de matrices. Introduzcamos la relación de equivalencia en (A+B)* siguiente:
El cociente
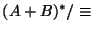 resulta ser un submonoide de
resulta ser un submonoide de
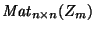 .
Escriba un programa que dados m y n y dos matrices
.
Escriba un programa que dados m y n y dos matrices
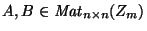 calcule a los elementos en
calcule a los elementos en
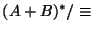 y a su tabla de multiplicación.
y a su tabla de multiplicación.
17. Dada una palabra
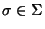 ,
un período es un prefijo
,
un período es un prefijo 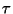 de
de  tal que
tal que  es un prefijo de alguna potencia de
es un prefijo de alguna potencia de 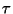 ,
es decir,
,
es decir,
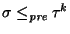 para alguna k.
Escriba un programa que dada una palabra
para alguna k.
Escriba un programa que dada una palabra  calcule todos sus períodos y escriba una lista de las longitudes de los períodos.
calcule todos sus períodos y escriba una lista de las longitudes de los períodos.
18. Una palabra
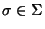 se dice ser libre-de-cuadrados si no contiene ningún enfijo de la forma
se dice ser libre-de-cuadrados si no contiene ningún enfijo de la forma 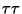 ,
con
,
con
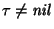 .
Escriba un programa que dados n y m escriba una lista de todas las palabras de longitud a lo sumo n que están libres de cuadrados sobre el alfabeto de m símbolos
.
Escriba un programa que dados n y m escriba una lista de todas las palabras de longitud a lo sumo n que están libres de cuadrados sobre el alfabeto de m símbolos
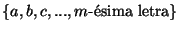 .
.
19. Sea A1=(a+b) el alfabeto consistente de dos símbolos, y sea
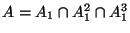 el lenguaje consistente de las 14 palabras de longitud a lo más 3 sobre A1.
el lenguaje consistente de las 14 palabras de longitud a lo más 3 sobre A1.
- 1.
- Escriba un programa que dados n y un subconjunto no vacío
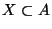 enliste al conjunto Xn conformado por las palabras de longitud a lo más n formadas al concatenar partículas en X.
enliste al conjunto Xn conformado por las palabras de longitud a lo más n formadas al concatenar partículas en X.
- 2.
- Para cada n defina la relación de equivalencia:
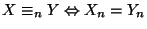 .
Escriba un programa que dado n escriba la matriz de adyacencia de
.
Escriba un programa que dado n escriba la matriz de adyacencia de 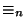 .
.
20. Dos palabras
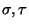 se dicen conjugadas si existe una tercer palabra
se dicen conjugadas si existe una tercer palabra 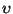 tal que
tal que
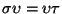 .
Esta relación es de equivalencia.
Escriba un programa que dados m y n dé las clases de equivalencia de la relación de conjugación restringida a las palabras de longitud n sobre un alfabeto de m símbolos.
Conjeture cuántas clases ha de haber, en términos de m y n.
.
Esta relación es de equivalencia.
Escriba un programa que dados m y n dé las clases de equivalencia de la relación de conjugación restringida a las palabras de longitud n sobre un alfabeto de m símbolos.
Conjeture cuántas clases ha de haber, en términos de m y n.
21. Escriba un programa que dados m, y dos palabras  y
y 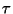 ,
sobre un alfabeto de m símbolos, donde
,
sobre un alfabeto de m símbolos, donde  antecede a
antecede a 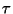 en el orden lexicográfico, calcule cuántas palabras están entre
en el orden lexicográfico, calcule cuántas palabras están entre  y
y 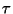 (contando a
(contando a 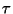 pero excluyendo a
pero excluyendo a  ,
según ese orden).
,
según ese orden).
22. Derivación guiada en gramáticas formales: Escriba un programa que dada una gramática formal
G=(V,T,P,s0) le permita a un usuario derivar de manera interactiva palabras, seleccionando producciones a aplicarse en partículas de la palabra actual.
En otras palabras, divida la pantalla en dos sectores, en cada uno de los cuales ha de poder hacerse ``scrolling''. En el primero se muestra las producciones enumeradas. En el segundo se deriva palabras. La palabra actual es la última línea de este segundo sector. El usuario ha de ``remarcar'' una partícula en la palabra actual, ha de indicar cuál producción quiere aplicar y el programa aplicará esa producción dejando el resultado como palabra actual.
23. Problema de la palabra en gramáticas libres de contexto: Escriba un programa que resuelva el Problema de la palabra en gramáticas libres de contexto, buscando derivaciones siniestras (``leftmost'').
Para una gramática libre de contexto
G=(V,T,P,s0) y una palabra dada  decida si acaso
decida si acaso
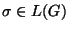 .
Si
.
Si
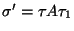 es una palabra que posee un prefijo común con
es una palabra que posee un prefijo común con  ,
,
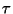 ,
consistente de símbolos terminales y A es un símbolo variable, entonces vea cuáles producciones con antecedente A tienen consecuentes que ``empaten'' con
,
consistente de símbolos terminales y A es un símbolo variable, entonces vea cuáles producciones con antecedente A tienen consecuentes que ``empaten'' con  .
Opte por las primeras. Proceda de esta forma hasta reconocer a
.
Opte por las primeras. Proceda de esta forma hasta reconocer a  .
Si fallara entonces realice ``backtracking'' considerando otras producciones que empaten con
.
Si fallara entonces realice ``backtracking'' considerando otras producciones que empaten con  .
.
24. Diseñe una gramática que genere al lenguaje
Escriba un programa que dado n muestre visualmente la manera en la que hay que aplicar las reglas para generar 12n.
25. Diseñe una gramática que genere al lenguaje
Escriba un programa que dado n muestre visualmente la manera en la que hay que aplicar las reglas para generar 1n2.
Sugerencia: Observe que para todo
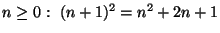 .
.
26. Diseñe una gramática que genere al lenguaje
Escriba un programa que dados i,j muestre visualmente la manera en la que hay que aplicar las reglas para generar
aibjaibj.
27. Considere a la gramática con producciones
Escriba un programa que dado 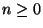 genere una palabra terminal de longitud 2n+1.
Escriba un programa que dado
genere una palabra terminal de longitud 2n+1.
Escriba un programa que dado 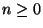 cuente el número total de derivaciones posibles para arribar a una palabra de longitud 2n+1.
cuente el número total de derivaciones posibles para arribar a una palabra de longitud 2n+1.
28. Cuenta de palabras en gramáticas libres de contexto: Escriba un programa que para una gramática libre de contexto
G=(V,T,P,s0) y para un número n cuente cuántas palabras de longitud n se derivan en G.




Siguiente: Autómatas finitos y expresiones
Un nivel arriba: Gramáticas formales
Anterior: Ejercicios
Guillermo Morales-Luna
2000-06-27