Siguiente: Monoides de autómas no-deterministas
Un nivel arriba: Nociones básicas
Anterior: Nociones básicas
Sea
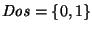 el álgebra booleana de dos elementos, dotada de sus operaciones usuales de conjunción, ``
el álgebra booleana de dos elementos, dotada de sus operaciones usuales de conjunción, ``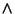 '' y disyunción, ``
'' y disyunción, ``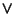 '':
'': 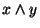 es 1 sólo si ambos x e y son 1;
es 1 sólo si ambos x e y son 1; 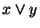 es 0 sólo si ambos x e y son 0.
Para cada símbolo de entrada
es 0 sólo si ambos x e y son 0.
Para cada símbolo de entrada
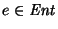 definamos la matriz
definamos la matriz
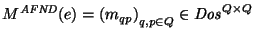 tal que para todos
tal que para todos 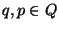 :
:
Similarmente, para
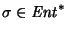 definamos la matriz
definamos la matriz
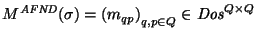 tal que para todos
tal que para todos 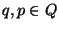 :
:
Así pues,
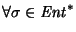 se tiene la relación,
se tiene la relación,
Ahora bien, la colección
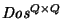 de matrices booleanas con índices en Q tiene una estructura de anillo con la operación suma dada por la disyunción entrada a entrada,
de matrices booleanas con índices en Q tiene una estructura de anillo con la operación suma dada por la disyunción entrada a entrada,
y el producto booleano de matrices,
Lema 3.1
Si
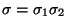
entonces
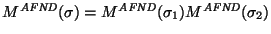
.
En particular, si
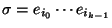
entonces
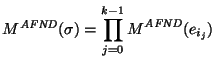
.
Ejemplo. Para el AFND del ejemplo anterior tenemos




Siguiente: Monoides de autómas no-deterministas
Un nivel arriba: Nociones básicas
Anterior: Nociones básicas
Guillermo Morales-Luna
2000-06-27
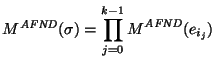 .
.