



Siguiente: Reconocimiento de lenguajes
Un nivel arriba: Autómatas de pila
Anterior: Autómatas de pila
Una pila es un dispositivo de almacenamiento que sigue el principio ``primero-en-entrar-último-en salir''. Lo podemos pensar como un arreglo lineal indicado con los números naturales:
La casilla c[0] se dice ser el tope de la pila. En todo momento,
Sobre una pila se pueden ejecutar dos operaciones:
- Empilar:
- Si
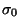 es una palabra en
es una palabra en
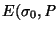 y
y
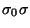 es el contenido de la pila, entonces la acción
es el contenido de la pila, entonces la acción
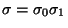 hace que el contenido de la pila sea
hace que el contenido de la pila sea
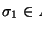 .
.
- Desempilar:
- Si
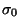 es un prefijo del contenido
es un prefijo del contenido
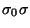 de la pila, es decir
de la pila, es decir
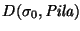 para alguna palabra
para alguna palabra
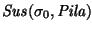 ,
entonces la acción
,
entonces la acción
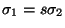 hace que el contenido de la pila sea
hace que el contenido de la pila sea 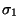 .
.
(Es convencional nombrar a las operaciones E y D por sus denotaciones en inglés: Push y Pop, respectivamente.)
Ahora bien, estas dos operaciones pueden realizarse mediante una operación de ``sustitución'' del tope de la pila:
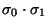 hace que si el contenido de la pila fuese
hace que si el contenido de la pila fuese
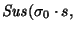 ,
donde s es el símbolo actual en el tope de la pila, entonces el contenido vendrá a ser
,
donde s es el símbolo actual en el tope de la pila, entonces el contenido vendrá a ser
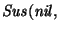 .
En otras palabras, el contenido del tope s es sustituído por
.
En otras palabras, el contenido del tope s es sustituído por 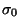 .
Así pues la acción
.
Así pues la acción
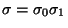 equivale a
equivale a
 ,
donde s es el contenido en el tope; en tanto que la acción
,
donde s es el contenido en el tope; en tanto que la acción
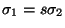 es equivalente a reiterar la acción
es equivalente a reiterar la acción
 tantas veces como sea la longitud de
tantas veces como sea la longitud de 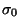 .
En el resto de esta sección consideraremos solamente acciones de sustitución en el tope de la pila.
Un autómata de pila (no-determinista) es una estructura de la forma
.
En el resto de esta sección consideraremos solamente acciones de sustitución en el tope de la pila.
Un autómata de pila (no-determinista) es una estructura de la forma
donde
En cada momento, el autómata funciona como sigue: Si se está en el estado 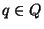 ,
se recibe el símbolo
,
se recibe el símbolo
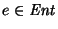 y en el tope de la pila se encuentra el símbolo
y en el tope de la pila se encuentra el símbolo
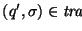 ,
,
- si
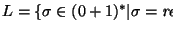 entonces se pasa al estado q', se sustituye Y por
entonces se pasa al estado q', se sustituye Y por  y NO se avanza en la cadena de entrada, o bien
y NO se avanza en la cadena de entrada, o bien
- si
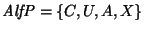 entonces se pasa al estado q', se opera en la pila según se describe arriba y se avanza una posición a la derecha en la cadena de entrada.
entonces se pasa al estado q', se opera en la pila según se describe arriba y se avanza una posición a la derecha en la cadena de entrada.
Ejemplo (Palíndromas):
Sea
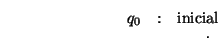 el lenguaje que consta de todas las palabras que son palíndromas.
Una estrategia obvia para reconocer palabras en L es la siguiente:
el lenguaje que consta de todas las palabras que son palíndromas.
Una estrategia obvia para reconocer palabras en L es la siguiente:
- 1.
- al inicio la pila ha de estar vacía,
- 2.
- se deposita en la pila una copia de ``la primera mitad de la palabra recibida'', es decir,
- (a)
- con cada 0 que llegue se coloca una marca C en la pila,
- (b)
- con cada 1 que llegue se coloca una marca U en la pila,
- 3.
- al (suponer) haber llegado la ``primera mitad'' se busca que ``la segunda'' empate con la primera, es decir,
- (a)
- se pasa a un estado de desempilar,
- (b)
- con cada 0 que llegue y que empate con una marca C en la pila, se desempila la marca,
- (c)
- con cada 1 que llegue y que empate con una marca U en la pila, se desempila la marca,
- 4.
- se tendrá éxito sólo si al terminar de leer se tiene vacía la pila.
Así pues, consideremos los conjuntos siguientes:
- Alfabeto de entrada:
-
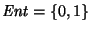 .
.
- Alfabeto de pila:
-
 .
X es la marca del extremo derecho de la pila. C y U son marcas para recontar 0's y 1's, y A es una marca de error.
.
X es la marca del extremo derecho de la pila. C y U son marcas para recontar 0's y 1's, y A es una marca de error.
- Estados:
- Consideremos 4 estados,
- Transiciones:
- Las siguientes transiciones se explican por sí solas. Las de la izquierda corresponden a ``buenas computaciones'' de reconocimiento. Las de la derecha marcan errores.
En cualquier otra configuración, la función de transición asocia el conjunto vacío.
Ejemplo:
Sea
 el lenguaje que consta de todas las palabras que bien son vacías o bien se inician con 0's, terminan con 1's y contienen el triple de 0's que de 1's.
Una estrategia obvia para reconocer palabras en L es la siguiente:
el lenguaje que consta de todas las palabras que bien son vacías o bien se inician con 0's, terminan con 1's y contienen el triple de 0's que de 1's.
Una estrategia obvia para reconocer palabras en L es la siguiente:
- 1.
- al inicio la pila ha de estar vacía,
- 2.
- con cada 0 que llegue se coloca una marca C en la pila,
- 3.
- al llegar al primer 1 se pasa a un estado de desempilar,
- 4.
- con cada 1 hay que desempilar exactamente 3 marcas C, y
- 5.
- se tendrá éxito sólo si al terminar de leer se tiene vacía la pila.
Así pues, consideremos los conjuntos siguientes:
- Alfabeto de entrada:
-
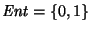 .
.
- Alfabeto de pila:
-
 .
X es la marca del extremo derecho de la pila. C es una marca para recontar 0's y A es una marca de error.
.
X es la marca del extremo derecho de la pila. C es una marca para recontar 0's y A es una marca de error.
- Estados:
- Consideremos 5 estados,
- Transiciones:
- Las siguientes transiciones se explican por sí solas. Las de la izquierda corresponden a ``buenas computaciones'' de reconocimiento. Las de la derecha marcan errores.
En cualquier otra configuración, la función de transición asocia el conjunto vacío.




Siguiente: Reconocimiento de lenguajes
Un nivel arriba: Autómatas de pila
Anterior: Autómatas de pila
Guillermo Morales-Luna
2000-06-27
 ,
donde s es el contenido en el tope; en tanto que la acción
,
donde s es el contenido en el tope; en tanto que la acción
 tantas veces como sea la longitud de
tantas veces como sea la longitud de