de Bruijn approach

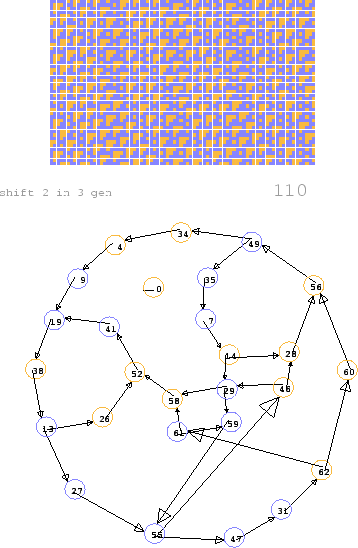
Figure 2.16: Cook's A-gliders and the de Bruijn diagram from which they may be derived. The outer periphery corresponds to the period-7, cycle 14 period rectangle of the ether tiles. If T3's and T1's alternate, there are three phases each of which has a cycle of length of 6. Also, if pure T1's run in succession, there is a loop of length 4 which will geberate them. Other mixtures correspond to other paths through the diagram.