Diagonal matrices

The eigenvectors of a matrix are expected to form a basis, something which is not always true but with exceptions which can be treated separately, or as limits. If we create a matrix U by writing a row of eigencolumns of M,

$$\begin{eqnarray*} U & = & \left[X_1, X_2, \ldots, X_n\right], \end{eqnarray*}$$

then submatrix multiplication gives the immediate result

$$\begin{eqnarray*} M U & = & \left[ M X_1, M X_2, \ldots, M X_n \right] , \\ &... ... . & . & . & . & . \end{array} \right] \\ & = & U \Lambda, \end{eqnarray*}$$

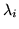where $\Lambda$ is a matrix full of zeroes except for its main diagonal, whose elements may also be zero, but usually are not. Such a matrix is called a diagonal matrixdiagonal matrix, satisfying the relationship $M U = U \Lambda$; such an equation is possible because the scalars $\lambda_i$ commute with the 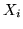$X_i$'s, even when the 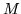$M$'s refuse.

Since U is a square matrix, it too is a mapping - one which transforms unit vectors into its columns - thereby making them into a basis of eigenvectors. Its inverse, V, goes in the other direction; from previous remarks, it can be described as a column of row eigenvectors, for which 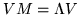$V M = \Lambda V$. Using 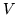$V$, changing bases for 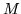$M$ leads to

$$\begin{eqnarray*} V M U & = & \Lambda, \end{eqnarray*}$$

a process which is called diagonalizing 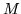$M$. From this it is apparent that the eigenvectors comprise the preferred basis for a matrix, although in reality we have to work with a reciprocal pair of bases, one for vectors and the other for components.