



Next: Fourier pairs
Up: Mappings Between Vector Spaces
Previous: Commuting matrices
Contents
A variant on commutation of matrices is anticommutation. As before, consider 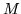 and N as two matrices for which
and N as two matrices for which
with X an eigenvector for M whereby
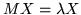 . Then
. Then
Either 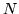 is singular,
is singular, 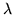 is zero (making
is zero (making 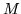 singular), or
singular), or 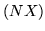 is another eigenvalue belonging to
is another eigenvalue belonging to 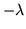 . Evidently the relationship is a mutual one,
. Evidently the relationship is a mutual one, 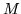 mapping eigenvectors of
mapping eigenvectors of 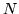 into new ones with reversed eigenvalue sign. We need to consider four regions: vectors annihilated by
into new ones with reversed eigenvalue sign. We need to consider four regions: vectors annihilated by 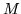 , vectors annihilated by
, vectors annihilated by 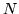 , the vectors with positive eigenvalue associated with
, the vectors with positive eigenvalue associated with 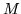 , and those with negative eigenvalues, conjugated from the first group by
, and those with negative eigenvalues, conjugated from the first group by 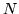 .
.
Setting up the explicit format of the previous section and repeating the derivation leads to the conclusion that
Various schematic representations of the situation are possible, but are probably best summarized by saying that M and N have the respective forms:
The 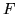 and
and 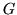 parts can be discarded except for singularity (but then the dimension of
parts can be discarded except for singularity (but then the dimension of 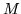 and
and 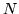 must be even), leaving the general impression that anticommuting matrices can be brought to a form with one of them diagonal, the other antidiagonal, and both with their nonzero eigenvalues arranged in negative pairs.
must be even), leaving the general impression that anticommuting matrices can be brought to a form with one of them diagonal, the other antidiagonal, and both with their nonzero eigenvalues arranged in negative pairs.




Next: Fourier pairs
Up: Mappings Between Vector Spaces
Previous: Commuting matrices
Contents
Pedro Hernandez
2004-02-28
![]() and N as two matrices for which
and N as two matrices for which
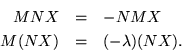
![\begin{eqnarray*}
\left[ \begin{array}{ll\vert l\vert l}
A & . & . & . \\
....
.... & . & . & . \\
\hline
. & . & . & G
\end{array} \right]
\end{eqnarray*}](img226.gif)