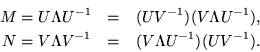It takes eigenvectors and eigenvalues to define a matrix. We have seen that the condition of having a common eigenvector set depends on whether two matrices commute or not. One could equally wonder whether there is an analogous relationship for matrices which have common sets of eigenvalues? Since the eigenvectors define a basis, the question is essentially one of how to recognize pairs of matrices whose only difference lies in the coordinate system in which they are defined. Suppose that ![]() and
and ![]() are two square matrices, and that
are two square matrices, and that ![]() defines a mapping between vector spaces (not necessarily the same one), in which case
defines a mapping between vector spaces (not necessarily the same one), in which case ![]() and
and ![]() could even have different dimensions.
could even have different dimensions.
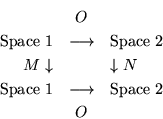
The required relationship is that
with the further relationship
So far it is just a question that ![]() and
and ![]() produce the same results, independently of the stage at which
produce the same results, independently of the stage at which ![]() is introduced, and nothing has been said about eigenvalues. Nevertheless note that if
is introduced, and nothing has been said about eigenvalues. Nevertheless note that if
![]() , we would have
, we would have
![]() whilst
whilst
![]() (indicating a use of the associative law by introducing parentheses). Altogether,
(indicating a use of the associative law by introducing parentheses). Altogether,
![]() , so that
, so that ![]() and
and ![]() can be expected to have matched eigenvectors with the same eigenvalue unless a singularity of
can be expected to have matched eigenvectors with the same eigenvalue unless a singularity of ![]() intervenes. To that extent,
intervenes. To that extent, ![]() and
and ![]() have the same eigenvalues.
have the same eigenvalues.
To observe the correspondence of the whole set of eigenvalues, suppose that ![]() diagonalizes
diagonalizes ![]() to
to ![]() and that
and that ![]() diagonalizes
diagonalizes ![]() to
to ![]() :
: