


Next: Band Matrices
Up: Mappings Between Vector Spaces
Previous: Matrices as vectors
Contents
Consider the fate of a Vandermonde determinant when two of its columns coincide, for example when a and b were nearly equal.
Starting from the determinant, we could subtract the a column from the b column,
and to save writing all the steps one by one, observe that 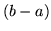 is now a common factor of all the terms in the third column except for the last which would leave
is now a common factor of all the terms in the third column except for the last which would leave
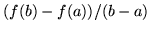 and a determinant whose neareness to zero depends on this factor. That suggests discarding the factor and recognizing a derivative. The result is called the confluent form of the Vandermonde determinant, leading to Hermite interpolation when used for that purpose. It is not excluded that several pairs of points coalesce, it just means using more derivatives as well as values at all those points. If three points condense, the second derivative can also be extracted from the assemblage, and so on for as many clusters as might appear.
and a determinant whose neareness to zero depends on this factor. That suggests discarding the factor and recognizing a derivative. The result is called the confluent form of the Vandermonde determinant, leading to Hermite interpolation when used for that purpose. It is not excluded that several pairs of points coalesce, it just means using more derivatives as well as values at all those points. If three points condense, the second derivative can also be extracted from the assemblage, and so on for as many clusters as might appear.
A similar limiting process reccommends itself when the characteristic equation of a polynomial has multiple roots, because the spectral decomposition of the matrix is essentially a Lagrange interpolation over the eigenvalues. Derivatives ought to begin to make their appearance.
To see how this works, pick out a simple 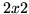 matrix, such as
matrix, such as
whose characteristic equation is
with roots
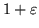 and
and
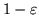 . Consequently, if
. Consequently, if 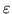 were near zero, there would be an approximate degeneracy.
were near zero, there would be an approximate degeneracy.
Two matrices of eigenvectors, left and right, are,
from which it appears that there is only one eignvector when
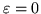 , and that that left eigenvector would be orthogonal to the only right eigenvector, precluding its normalization to unit projection.
, and that that left eigenvector would be orthogonal to the only right eigenvector, precluding its normalization to unit projection.
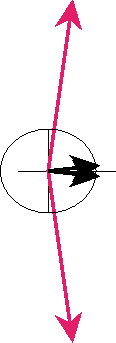
Figure:
Confluence of eigenvectors in the Jordan Normal Form, showing how the left eigenvector becomes orthogonal to its own right eigenvector.
 |



Next: Band Matrices
Up: Mappings Between Vector Spaces
Previous: Matrices as vectors
Contents
Pedro Hernandez
2004-02-28
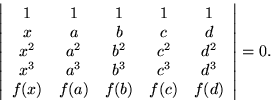
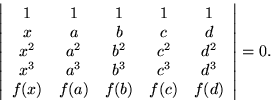
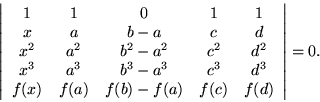
![]() matrix, such as
matrix, such as
