



Next: quaternion inverse
Up: A uniform treatment for
Previous: A uniform treatment for
Contents
The best way to get this point of view, and at the same time give the whole topic of 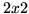 matrices an elegent formulation, is to use quaternions. Starting from the natural basis for
matrices an elegent formulation, is to use quaternions. Starting from the natural basis for 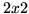 matrices,
matrices,
whose rule of multiplication is
 , quaternion-like matrices can be defined by
, quaternion-like matrices can be defined by
In detail,
all built from sums and differences, thereby retaining real matrices. Like quaternions, these matrices anticommute (except for the identity), so the difference is that only one square is 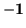 , the others are
, the others are 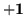 . Because of that, exponentials will follow Euler'sEuler's formula formula by using either trigonometric or hyperbolic functions according to the sign.
. Because of that, exponentials will follow Euler'sEuler's formula formula by using either trigonometric or hyperbolic functions according to the sign.
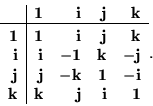
The multiplication table is
The usual way of performing algebraic operations on these matrices is to write a sum such as
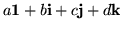 in the form
in the form 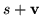 , where
, where 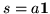 and
and 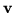 is the rest of the sum. Doing that allows writing
is the rest of the sum. Doing that allows writing
particular interest attaching to the case where  and
and  are zero, leaving the product of two vectors to take the form of a scalar plus a vector. However, the inner (or dot) product is not the usual one, rather one with a MinkowskiMinkowski metric type metric:
are zero, leaving the product of two vectors to take the form of a scalar plus a vector. However, the inner (or dot) product is not the usual one, rather one with a MinkowskiMinkowski metric type metric:
Since the inner product for a Minkowski metric can be positive, negative, or zero, taking it for the square of a norm requires considering the sign, unless an imaginary norm is acceptable. So to define the norm of a vector, use the absolute value of the metric, by setting
note that it can vanish for a nonzero vector, and never forget the possible influence of the bypassed sign.
In turn the vector product differs slightly from its cartesian version. It is
The latter formula, almost traditional, abuses determinantal notation. But this particular formula never implies any multiplication of quaternions, so it works out well enough, although differing from the classical formula in the sign of the term associated with 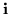 .
.




Next: quaternion inverse
Up: A uniform treatment for
Previous: A uniform treatment for
Contents
Pedro Hernandez
2004-02-28
![]() matrices an elegent formulation, is to use quaternions. Starting from the natural basis for
matrices an elegent formulation, is to use quaternions. Starting from the natural basis for ![]() matrices,
matrices,
![\begin{eqnarray*}
{\bf e}_{11} & = & \left[ \begin{array}{cc} 1 & 0 \\ 0 & 0 \en...
... & \left[ \begin{array}{cc} 0 & 0 \\ 0 & 1 \end{array} \right].
\end{eqnarray*}](img362.gif)
![\begin{eqnarray*}
{\bf 1}& = & \left[ \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{arr...
...& \left[ \begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array} \right].
\end{eqnarray*}](img364.gif)
![\begin{eqnarray*}
({\bf u}\cdot {\bf v}) & = & - u_1 v_1 + u_2 v_2 + u_3 v_3, \...
...t[ \begin{array}{c}
v_1 \\ v _2 \\ v_3
\end{array} \right].
\end{eqnarray*}](img377.gif)

![]() .
.