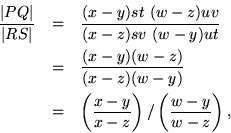matrix interpretation

Consider the projective line as an image of a two-dimensional linear algebra plane, and observe that determinants are multiplicative for linear transformations. Take a $2 \times 2$ matrix $P$ containing the two columns of a basis and a transformation $M$. Then $\vert MP\vert=\vert M\vert\vert P\vert$, so $\vert P\vert$ is not an invariant. But take another basis matrix $Q$ for which $\vert MQ\vert=\vert M\vert\vert Q\vert$. Then the quotient $\vert P\vert/\vert Q\vert$ is invariant, although its terms are not.

Figure: Pappus' construction for the invariance of the cross ratio. It would take a more cartesian form if the projection point were moved to the origin and one of the lines were $y=1$. As a scheme for mapping lines, this is not a projection of a plane to a line; however it is a 1:1 mapping of one line to another.

Carrying the result over to the projective line, write the matrices in projective form

$$P = \left[ \begin{array}{cc} xs & yt \\ s & t \end{array} \ri... ...left[ \begin{array}{cc} wu & zv \\ u & v \end{array} \right],$$

and calculate the determinants. Note that $w, x, y, z$ are the values of points on the projective line, whereas $s, t, v, u$ are the multipliers lost by the projection. We have

$$\begin{eqnarray*} \frac{\vert P\vert}{\vert Q\vert} & = & \frac{(x-y)st}{(w-z)uv} \end{eqnarray*}$$

Although this quotient is invariant enough, the multipliers would normally be unknown. Choosing more vectors and dividing once again would only create more multipliers, but the same multipliers can be kept by just rearranging the four vectors in the two bases. There are twenty four possibilities, the permutations of four objects, but only some of them produce the cancellation which would free the points from the multipliers.

The nice symmetry of the formula shows how to get the cancellation; note that each difference is multiplied by the product of its two multipliers. Making up a product of four multipliers in two different ways would allow cancelling the unknown factors while retaining the differences in the points themselves.

So make up two new matrices,

$$R = \left[ \begin{array}{cc} xs & zv \\ s & v \end{array} \ri... ...left[ \begin{array}{cc} wu & yt \\ u & t \end{array} \right].$$

The combination which we actually want is

$$\begin{eqnarray*} \frac{\vert PQ\vert}{\vert RS\vert} & = & \frac{(x-y)st\ (w-z... ... = & \left(\frac{x-y}{x-z}\right)/\left(\frac{w-y}{w-z}\right), \end{eqnarray*}$$

which is the quotient of quotients of distances from the customary formula to be found in all textbooks.