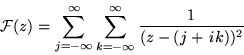
Macsyma es un paquete matemático que permite realizar computaciones aritméticas, simbólicas, además tiene una interfaz gráfica y permite incorporar programas escritos en FORTRAN. El programa de Macsyma que utilizamos es PC Macsyma (Macsyma 2.0).
En en calpítulo referente al análisis de la función se mencionó
que la expresión que se desea analizar es:
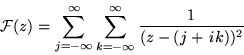
Para empezar debemos representar a ![]() como una función compleja.
Para lo cual primero debemos declarar a z como un número complejo
de la siguiente forma:
como una función compleja.
Para lo cual primero debemos declarar a z como un número complejo
de la siguiente forma:
(c1) z:a + %i*b$Donde (c1) es un número de línea de comando que el usuario ejecuta, z es el nombre de la varible, : es el símbolo que representa una declaración de variable,
a+%i*b es la expresión para
z, particularmente %i representa la parte imaginaria de la
expresión. El símbolo $ significa que z debe declararse y
no mostrarse en la terminal6.1.
Una vez declarada z como un número complejo, entonces se procede a declarar a f como la función que deseamos.
(c2) f(z) := sum(sum(1/(z-(j+%i*k))^2, j, -10, 10), k, -10, 10)$
Note que una función se declara con el símbolo = y no con : (como
el caso de las variables). La función sum() tiene la siguiente
sintaxis:
sum( expresion , variable, minimo, maximo)
La definición de ![]() no representa problemas para cálculos de
límites y otras computaciones algebráicas, pero la función
para graficar tiene problemas por la definición de z, por lo que se
decidió partir la función en su parte real y su parte imaginaria:
no representa problemas para cálculos de
límites y otras computaciones algebráicas, pero la función
para graficar tiene problemas por la definición de z, por lo que se
decidió partir la función en su parte real y su parte imaginaria:
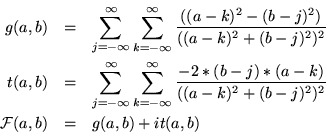
(c4) g(a,b) := sum(sum(((a-k)^2-(b-j)^2)/((a-k)^2+(b-j)^2)^2,j,-1,1),k,-1,1)$ (c5) t(a,b) := sum(sum(-2*(b-j)*(a-k)/((a-k)^2+(b-j)^2)^2 ,j,-1,1),k,-1,1)$ (c6) f(a,b) := f(a,b) := cabs( g(a,b) + %i*t(a,b))$
Posteriormente, para graficar la expresión utlizamos la siguiente secuencia de instrucciones:
(c7) contours:30$ (c8) labelcontours:true$ (c9) contourplot(f(a,b), a, -2,2, b,-2,2);
Donde contours indica el número de superfices de nivel que deseamos observar en la figura; labelcontours:true muestra las etiquetas para cada contorno y; contourplot manda a graficar los contornos de la función.