



Next: mapping the real line
Up: Mapping theorems
Previous: Mapping theorems
An already existing linear relationship, such as the expansion of a polynomial of nth degree in terms of powers xi of degrees zero through n,
| p(x) |
= |
 |
(211) |
can be written as the inner product of two vectors, say a row of coefficients
 and a column of powers,
and a column of powers,
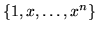 .
Any change of basis, such as by replacing powers xi with Newton polynomials
.
Any change of basis, such as by replacing powers xi with Newton polynomials
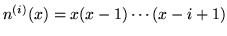 ,
gotten by linear transformation, would be represented by a matrix whose inverse transforms the coeffients, keeping the representation intact.
,
gotten by linear transformation, would be represented by a matrix whose inverse transforms the coeffients, keeping the representation intact.
If the expansion is not available, but it is desired to have a certain basis together with a family of linear functionals from which the coefficients are obtained, there is a determinant which can be used. For example, the combination of powers 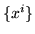 and values at a set of points
and values at a set of points
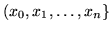 will produce the Lagrange interpolation polynomials via the Vandermonde determinant. Write
will produce the Lagrange interpolation polynomials via the Vandermonde determinant. Write
 |
= 0. |
|
(212) |
The rows correspond to basis elements, the columns to linear functionals; the vanishing of the determinant results from duplicating a column whenever the value of the functional at the additional point matches the interpolation. Assigning suitable names to the pieces resulting from partitioning the determinant according to its last row and column, and the corresponding Laplace development, the equation reads
This time there is a metric matrix which has to be calculated by inverting the matrix of mutual interactions, which will be possible if the two sets of constituents are actually linearly independent and form bases. The resulting representation formula will always work, but the question of its convergence as the number of reference points increases is usually fairly complicated. With power or polynomial bases, the degree of the polynomials is correspondingly high leaving the interior of the convex hull of the points as the only region in which a useful approximation should be expected. Whether that expectation can be realized, and many other points of interest, are discussed in Walsh's Colloquium Publication [27].




Next: mapping the real line
Up: Mapping theorems
Previous: Mapping theorems
Microcomputadoras
2001-04-05


![]() and values at a set of points
and values at a set of points
![]() will produce the Lagrange interpolation polynomials via the Vandermonde determinant. Write
will produce the Lagrange interpolation polynomials via the Vandermonde determinant. Write
