| Z(t) - Z(0) | = | 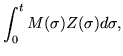 |
(237) |
One way to obtain a representation for the solution of a system of equations is to integrate the equation
dZ/dt = MZ, transforming it into an integral equation,
| Z(t) - Z(0) | = | 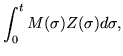 |
(237) |
| Z(t) | = | 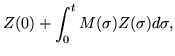 |
(238) |
| = | ![$\displaystyle Z(0) + \int_0^t M(\sigma) \left[ Z(0) +
\int_0^{\sigma} M(\sigma_1)Z(\sigma_1)d\sigma_1 \right]d\sigma,$](img403.gif) |
(239) | |
| = | ![$\displaystyle Z(0) + \int_0^t M(\sigma) \left[ Z(0) +
\int_0^{\sigma} M(\sigma_...
...t_0^{\sigma_1} M(\sigma_2)Z(\sigma_2)d\sigma_2 \right]d\sigma_1 \right]d\sigma,$](img404.gif) |
(240) | |
| = | ![$\displaystyle \left[ I + \int_0^t M(\sigma)Z(\sigma)d\sigma +
\int_0^t\int_0^{_\sigma}M(\sigma)M(\sigma_1)d\sigma_1d\sigma
+ \ldots\right]Z(0)$](img405.gif) |
(241) | |
| = | (242) |
This final matrix series, called a matrizant, possesses properties very similar to those of the matrix exponential. For example, by bounding the individual matrix elements and using the comparison test, it can be seen to converge as well as the exponential series.
If the coefficient matrix commutes for all values of its argument, for example when it is a matrix of constants, the ordering implicit in the nesting of the
variables of integration can be relaxed by extending each integral to the full range ![]() .
Then, dividing the resulting n-fold integral by the exponentially increasing n! to compensate the ensuing repetition by permutation of the basic domain of integration, the series simplifies to
.
Then, dividing the resulting n-fold integral by the exponentially increasing n! to compensate the ensuing repetition by permutation of the basic domain of integration, the series simplifies to
| Z(t) | = | ![$\displaystyle \left[ I + \int_0^t M(\sigma)Z(\sigma)d\sigma +
\frac{1}{2}\int_0^t\int_0^tM(\sigma)M(\sigma_1)d\sigma_1d\sigma
+ \ldots\right]Z(0)$](img408.gif) |
(243) |
| = | ![$\displaystyle \left[ I + \int_0^t M(\sigma)Z(\sigma)d\sigma +
\frac{1}{2}\left(\int_0^t M(\sigma)d\sigma\right)^2
+ \ldots\right]Z(0)$](img409.gif) |
(244) | |
| = | 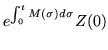 |
(245) |
The iterative process just descrined is known as Picard's method for solving differential equations. The gradual disappearance of the residual term from the result depends upon bounding the elements of the coefficient matrix as well as the rapidly diminishing volume of integration, which only encompasses the one ordered subset of the unit cube, whose volume is 1/n!. Still, the error term must sometimes be retained. In general, linear systems should be solved in regions free of singularities in the coefficients; one way to take advantage of the complex plane is to integrate along trajectories which avoid the singularity.
The actual singularity can sometimes be confronted by taking limits, as can the problems at infinity arising from bounded coefficients which nevertheless increase as infinity is approached.