One of the most insightful visual techniques is to introduce polar coordinates into the phase plane; it is called Prüfer's transformation
| = | 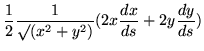 |
(285) | |
| = | 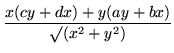 |
(286) | |
| = | (287) |
| = | 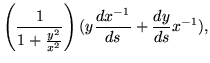 |
(288) | |
| = |  |
(289) | |
| = | x (ay + bx) - y (cy + dx) | (290) | |
| = | (291) |
| = | (292) | ||
| = | (293) |
| = | 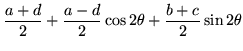 |
(294) | |
| = |  |
(295) |
An interesting comparison and check results from setting V = 0 in the matrix of the Schrödinger equation, Eq. (283). Then a = d = 0, b=-E and c=1. The Prüfer equations are
| = | (296) | ||
| = | (297) |
| = | (298) | ||
| = | (299) |
Often the Prüfer equations are not pursued beyond the ![]() -equation because the sign and magnitude of the derivative establish the oscillatory nature of the solutions. If the derivative is of constant sign and bounded away from zero, the solutions will
necessarily oscillate indefinitely with a period implied by the bound. Moreover, given two equations -- say the same equation with different values of the eigenvalue parameter E -- if the derivative of one of them is always greater than that of the other, conclusions about the interlacing of nodes can be drawn.
-equation because the sign and magnitude of the derivative establish the oscillatory nature of the solutions. If the derivative is of constant sign and bounded away from zero, the solutions will
necessarily oscillate indefinitely with a period implied by the bound. Moreover, given two equations -- say the same equation with different values of the eigenvalue parameter E -- if the derivative of one of them is always greater than that of the other, conclusions about the interlacing of nodes can be drawn.
Even in the simple example shown, there is an unexpected jitter in the angle ![]() ,
when the result is compared to the more familiar solution consisting of sines and cosines derived from uniform motion around the circumference of a circle, at an angular velocity which is the square root of E, not E itself. However, the result shown is not incorrect, and can be used to illustrate the advantages of preparing a system of differential equations for the optimal interpretation of results.
,
when the result is compared to the more familiar solution consisting of sines and cosines derived from uniform motion around the circumference of a circle, at an angular velocity which is the square root of E, not E itself. However, the result shown is not incorrect, and can be used to illustrate the advantages of preparing a system of differential equations for the optimal interpretation of results.
In this case, the coefficient of the differential equation is not a multiple of the quaternion ![]() whose exponential produces a simple rotation, but contains and admixture of the quaternion
whose exponential produces a simple rotation, but contains and admixture of the quaternion ![]() which would generate hyperbolic motion. The combination leads to an ellipse in the phase plane, rather than a circle. Furthermore, the expected
which would generate hyperbolic motion. The combination leads to an ellipse in the phase plane, rather than a circle. Furthermore, the expected ![]() is the quaternion norm of the coefficient, whilst terms such as
is the quaternion norm of the coefficient, whilst terms such as ![]() are the coefficients of the individual unit quaternions.
are the coefficients of the individual unit quaternions.
An appropriate preparation for the Prüfer transformation, actually one close to the self-adjoint form which is the version originally proposed by Prüfer, is to revise the matrix equation by writing

It then follows that
| = | 0 | (300) | |
| = | -1 | (301) |