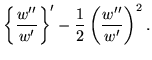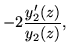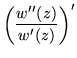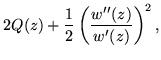solving a Schwartz derivative

A computation related to the link between a second order linear differential equation and a Ricatti equation gives a solution to a Schwartz differential equation

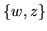$$\{w,z\}$$ = 2Q(z) (314)

where

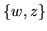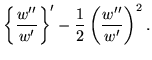$$\{w,z\} \left\{\frac{w''}{w'}\right\}'-\frac{1}{2}\left(\frac{w''}{w'}\right)^2.$$ = (315)

Suppose that y₁ and y₂ are two solutions of the second order equation

y'' + 2Q(z) = 0 (316)

whose nonvanishing and linear indepencence is established by their having a unit Wronskian,

$$\left\vert \begin{array}{cc} y_1(z) & y_2(z) \\ y_1'(z) & y_2'(z) \end{array}\right\vert$$ = 1. (317)

Starting with the definition

$$\frac{y_1(z)}{y_2(z)},$$ w(z) = 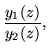(318)

there follow

w'(z) = [y₂(z)]^-2, (319)

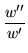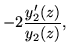$$\frac{w''}{w'} -2\frac{y_2'(z)}{y_2(z)},$$ = (320)

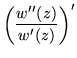$$\left(\frac{w''(z)}{w'(z)}\right)' -2\frac{y_2(z)'}{y_2(z)} + 2\left(\frac{y_2'(z)}{y_2(z)}\right)^2,$$ = (321)

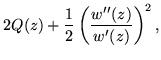$$2Q(z) + \frac{1}{2}\left(\frac{w''(z)}{w'(z)}\right)^2,$$ = (322)

according to which such a quotient solves the equation. The involvement of the Ricatti equation arises from concluding that the only other solutions of the Schwartz equation result from a change of basis from the two solutions y₁(z) and y₂(z), which would enter w in the form of a fractional linear transformation. But we already know that invariance under fractional linear transformation and invariance of the Schwartz derivative are two sides of the same coin.