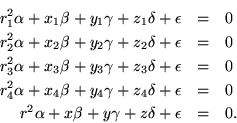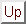


Next: A sphere orthogonal to
Up: Quartets of spheres
Previous: Quartets of spheres
Contents
To see how this philosophy works, consider four prescribed points
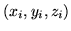 , a fifth arbitrary point
, a fifth arbitrary point 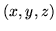 and the
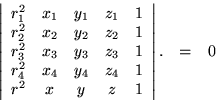
set of five equations which assert that these five points all lie on
the surface of a sphere (setting
and the
set of five equations which assert that these five points all lie on
the surface of a sphere (setting
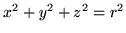 ):
):
The singularity of the coefficient matrix requires that
Laplace's expansion of this determinant according to its last row yields
explicit values for the coefficients
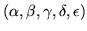 . Numerically, relatively
arbitrary values can be placed it the last row, and the whole matrix
inverted; we want the last row of the inverse, which is insensitive
to such choices.
. Numerically, relatively
arbitrary values can be placed it the last row, and the whole matrix
inverted; we want the last row of the inverse, which is insensitive
to such choices.
Pedro Hernandez
2004-05-13
![]() , a fifth arbitrary point
, a fifth arbitrary point ![]() and the
set of five equations which assert that these five points all lie on
the surface of a sphere (setting
and the
set of five equations which assert that these five points all lie on
the surface of a sphere (setting
![]() ):
):