 |
Spheres are amongst the most symmetrical of objects, so it is not surprising that projective geometry reserves an especially elegant place for them. There is a metric matrix for their coefficients wherein the norm of a sphere is its radius, and the angle between two sphere-vectors turns out to be the angle at which the spheres intersect.
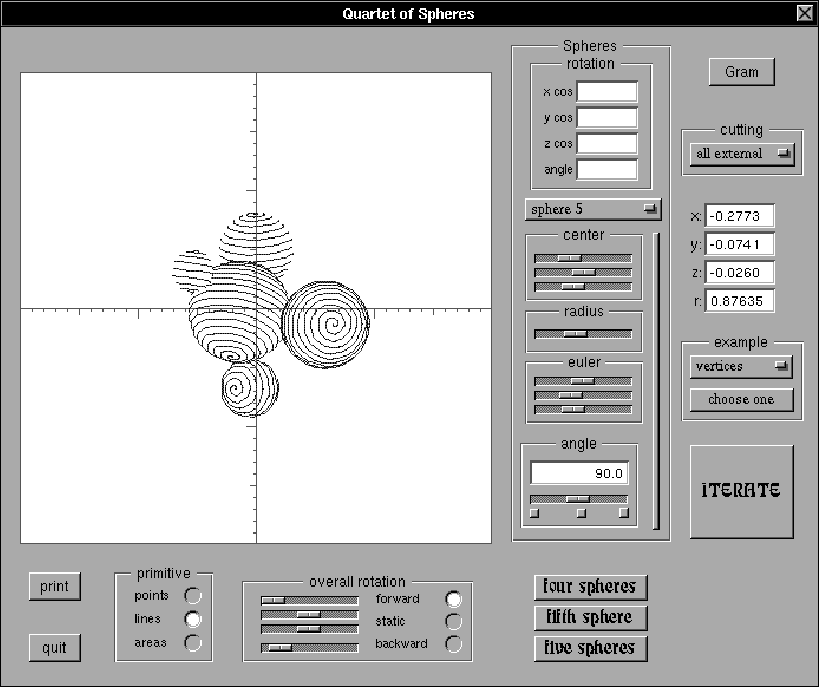
This brings up the three dimensional version of the ancient construction of the circle tangent to any three others. Sometimes the circle is imaginary, but in generality there are eight solutions, depending upon whether any given tangency is internal or external.
Apparently there are sixteen combinations possible for four spheres, but the construction can be generalized still further, wherein the angle with which each sphere intersects the fifth sphere can specified independently of the others. In particular, a real orthogonal fifth sphere can always be found, with the help of a simple matrix inversion.
 |