Spiral makes turnover flexagon

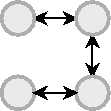
With these ideas it is possible to go ahead and make flexagons. But there are so many of them that the idea soon gets boring, in spite of all the time and effort which went into deducing the description in the first place. Given that one of the uses of flexagons is in magic shows (that is how Martin Gardner became involved with them) it is worthwhile looking for some simple yet striking combinations. One of them has a Tuckerman Tree which is a spiral; with four nodes it has the form

which could continue for still more turns but then would be hard to draw in ASCII. Anyway four is enough to talk about and see how it works.

The middle diagram of (square) cycles would be

In the ASCII drawing the line of ='s implies that the top square is not joined to the bottom square, which is also why the Tuckerman Tree does not connect to itself on the left (a Tree has no cycles, which is another consequence of the way flexagons are formed). For that reason points 10 and 2 are distinct from each other; it is easy to separate them in the line drawing.

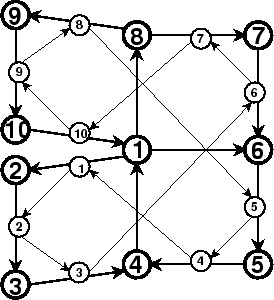
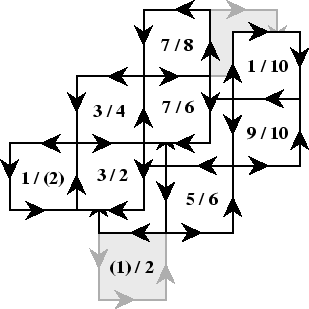
The detail which makes this class of flexagons, which are called spirals, interesting is that the point 1 is a part of every square, and so it is possible to return to it over and over as the flexagon is run through its paces. In fact, the construction is so nice that extremely long spirals can be constructed. By flexing, then turning over, the square packets fanfold and avoid the bulkiness of scrolling. The turning over is because of the arrows, which can only be respected by turning over.

The list of turns and faces would then be

+	+	+	+	+	-	-	-	-	-	+
1	3	3	7	7	1	9	9	5	5	1
2	2	4	6	8	10	10	8	6	4	2

from which the attendant frieze would be

or rather, this is half of it.