Next: Binary Hexagonal Flexagon Up: Hexagon Flexagons Previous: Introduction

First Level Hexagonal Flexagon

**Figure 1:** The first level hexagonal flexagon has 6 vertices.
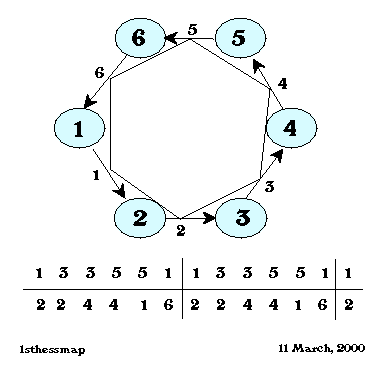$\begin{figure} \centering \begin{picture} (250,250) \put(0,0){\epsfxsize=250pt \epsffile{1sthessmap.eps}} \end{picture} \end{figure}$

**Figure 2:** Permutation of the hexagons along the strip for a first level hexagonal flexagon.
$\begin{figure} \centering \begin{picture} (200,200) \put(0,0){\epsfxsize=200pt \epsffile{hex1levper.eps}} \end{picture} \end{figure}$

**Figure 3:** Top side of a hexagonal flexagon consisting of a single cycle.
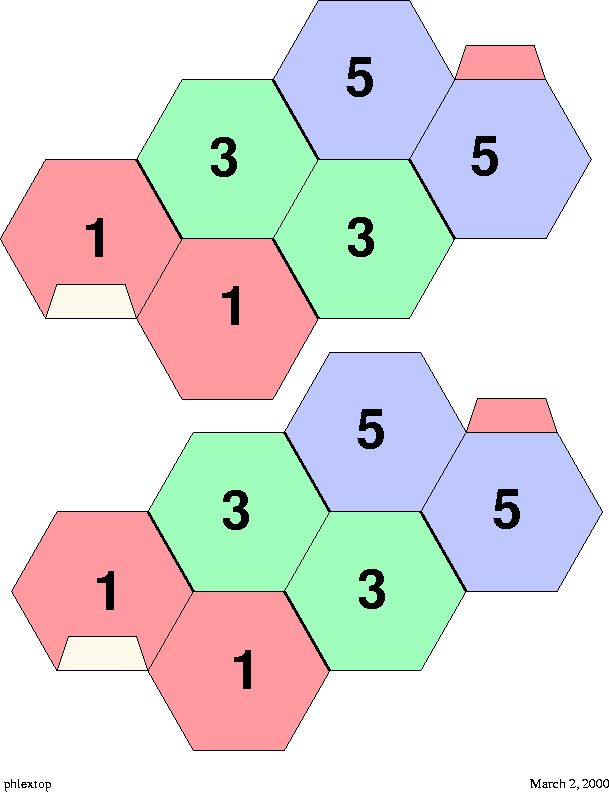$\begin{figure} \centering \begin{picture} (400,500) \put(0,0){\epsfxsize=400pt \epsffile{phlextop.eps}} \end{picture} \end{figure}$

**Figure 4:** Bottom side of a hexagonal flexagon consisting of a single cycle.
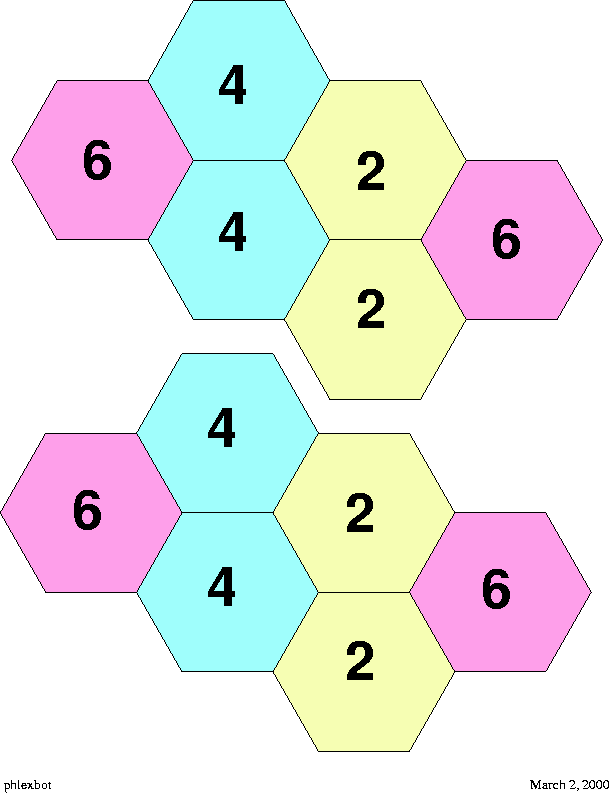$\begin{figure} \centering \begin{picture} (400,500) \put(0,0){\epsfxsize=400pt \epsffile{phlexbot.eps}} \end{picture} \end{figure}$

**Figure 5:** Top side of a hexagonal flexagon whose hexagon has been squared up.
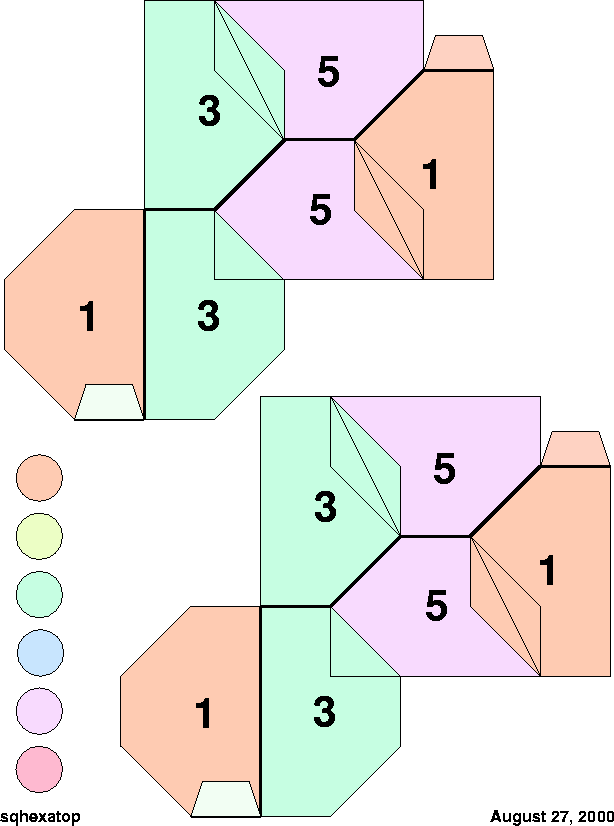$\begin{figure} \centering \begin{picture} (380,520) \put(0,0){\epsfxsize=400pt \epsffile{sqhexatop.eps}} \end{picture} \end{figure}$

**Figure 6:** Bottom side of a hexagonal flexagon whose gexagon has been squared up.
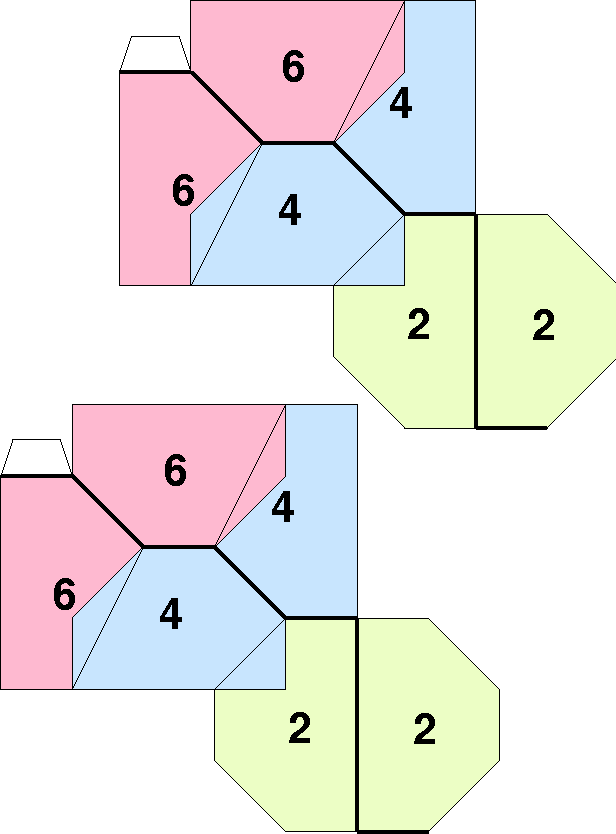$\begin{figure} \centering \begin{picture} (380,530) \put(0,0){\epsfxsize=400pt \epsffile{sqhexabot.eps}} \end{picture} \end{figure}$

Microcomputadoras
2000-11-02