 |
The solution of equations by iteration has a long history; once upon a time the main emphasis was on finding good initial approximations and convergence criteria, but nowadays computer experiments have shown that there are intricate global properties related to nonconvergence and the stability of convergence which are equally interesting and important.
The behavior of quadratic functions, the simplest of all nonlinear mappings, combines ease of calculation with sufficient generality to illustrate most of the abstract properties of iterations. Just as using complex variables often clarifies the properties of functions of a real variable, studying complex iterations can be expected to generalize and illuminate real nonlinear mappings as well.
Julia curves and Fatou sets are very intricate fixed sets belonging to complex mappings, whose structure summarizes many of the properties of real mappings. In turn the Mandelbrot set provides a map of the Julia curves, by use of which their appearance can be classified.
Several very interesting books of pictures have been published relating to these topics, some of which are listed in the bibliography.
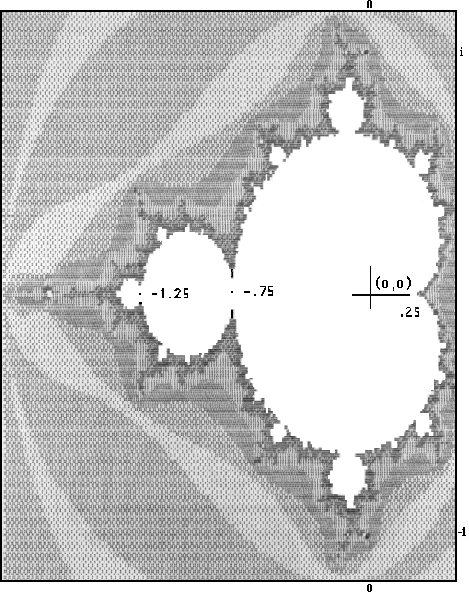
Figure 1 shows the Mandelbrot set, which serves as an overall guide to
the Julia curves. The main lobe is a cardioid, running from -0.75 to
0.25, so that the origin is about 3/4 of the way across the figure. The
tangent blobs are actually circles; additionally there are filamentary
tentacles with copies of the complete Mandelbrot figure strung along
them. They are not particularly evident at the resolution of the
figure, but are responsible for considering the Mandelbrot set to be
fractal.
Since the screen dump distorts the vertical scale, unit distance is almost the full height of the figure. The point i sits out on one tentacle, and corresponds to a limiting Julia curve which is a mere skeleton without an interior.
Figure 2 shows a Julia curve taken from the main blob. All Julia curves taken from the main blob are similar to a circle, which appears more and more pinched as its parameter approaches the boundary of the blob. The number of pinches will depend on the direction of the boundary point as seen from the origin. What we are actually dealing with is a fixed point which is stable. Therefore an iterative trajectory will approach it unless it is strictly periodic, or unless it converges to zero or infinity. Out in the tangent bubbles, the fixed point is unstable, but it has stable iterates. Just which iterates are stable depends upon the bubble in question, but their order is higher, the further out from the main bubble they are located.
Figure 3 shows another curve. The parameter of the first curve was taken from the negative real axis; that of the second from the vicinity of the imaginary axis. The curve arising from the complex conjugate of a parameter is the complex conjugate of the curve arising from the original parameter. Thus the curves arising from a real parameter have a symmetry by reflection in the real axis. Along the real axis, positive parameters lead to a squared up and vertically exaggerated circle; along the negative axis is is stretched horizontally and compressed vertically.