Bibliography

1

Eugene Jahnke and Fritz Emde, Tables of Functions with Formulae and Curves, Dover Publications, New York, 1945. Chapter XI.

2

E. T. Whittaker and G. N. Watson, A Course of Modern Analysis, Cambridge, at the University Press, 1927. Chapter XIX.

3

Milton Abramowitz and Irene Stgegun (editors), Handbook of Mathematical Functions, U. S. Government Printing Office, Washington D. C., 1964. Chapter 20.

4

R. de L. Kronig and W. G. Penney, ``Quantum Mechanics of Electrons in Crystal Lattices,'' Proceedings of the Royal Society (London) A 130 499-513 (1931).

5

W. Kohn, ``Analytic Properties of Bloch Waves and Wannier Functions,'' Physical Review 115 809-821 (1959).

6

Harold V. McIntosh, ``Quantization as an Eigenvalue Problem,'' In Group Theory and Its Applications, Vol. 3, (Ernest M. Loebl Editor), Academic Press pp. 333-368 (1975)

7

Harold V. McIntosh, ``Quantization and Green's Function for Systems of Linear Ordinary Differential Equations,'' In Quantum Science: Methods and Structure, Edited by J. L. Calais, O. Goscinsky. J. Linderberg and Y. Ohrn, Plenum Press, New York, pp. 227-294 (1976).

8

Bill Sutherland and Daniel C. Mattis, ``Ambiguities with the relativistic delta-function potential,'' Physical Review A 24 1194-1197 (1981).

9

F. Domínguez Adame, ``Relativistic and nonrelativistic Kronig-Penney models,'' American Journal of Physics 55 1003-1006 (1987).

10

Bruce H. J. McKellar and G. J. Stephenson, Jr., ``Klein Paradox and the Dirac-Kronig-Penney model,'' Physical Review A 36 2566-2569 (1987).

11

W. Glöckle, Y. Nogami, and I. Fukui, ``Structure of a composite system in motion in relativistic quantum mechanics,'' Physical Review D 35 584-590 (1987).

12

F. A. B. Continho, Y. Nogami, and F. M. Toyama, ``General aspects of the bound-state solutions of the one-dimensional Dirac equation,'' American Journal of Physics 56 904-907 (1988).

13

F. Domínguez Adame and E. Macía, ``On Relativistic Singular Harmonic-Oscillator Potentials,'' Europhysics Letters 8 711-715 (1989).

14

F. Domínguez Adame ``A generalized Dirac-Kronig-Penney model,'' J. Phys Condens. Matter 1 109-112 (1989).

15

F. Domínguez-Adame and E. Maciá, ``Bound states and confining properties of relativistic point interaction potentials,'' J. Phys. A: Math. Gen. 22 L419-L423 (1989).

16

F. Domínguez Adame and M. A. González ``Solvable Linear Potentials in the Dirac Equation,'' Europhysics Letters 13 193-198 (1990).

17

B. Méndez and F. Domínguez Adame, ``A simple numerical method for the determination of relativistic one-dimensional band structures,'' J. Phys A: Math. Gen. 24 L331-L336 (1991).

18

E. Macía and F. Domínguez Adame, ``Scattering states of relativistic point interaction potentials,'' J. Phys. A: Math. Gen. 24 59-69 (1991).

19

F. Domínguez Adame, ``A relativistic interaction without Klein paradox,'' Physics Letters A 162 18-20 (1992).

20

B. Méndez, F. Domínguez Adame and E. Macía, ``A transfer matrix method for the determination of one-dimensional band structures,'' J. Phys A: Math. Gen. 26 171-177 (1993).

21

D. W. L. Sprung, Hua Wu and J. Martorell, ``Scattering by a finite periodic potential,'' American Journal of Physics 61 1118-1124 (1993).

22

S. L. Blundell, ``The Dirac Comb and the Kronig-Penney model: Comment on ``Scattering from a locally periodic potential,'' by D. J. Griffiths and N. F. Taussig [Am. J. Phys. 60 883-888 (1992),'' American Journal of Physics 61 1147-1148 (1993).

23

S. H. Patil, ``Completeness of the energy eigenfunctions for the one-dimensional 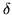$\delta$-function potential,'' American Journal of Physics 68 712-714 (2000).

24

D. W. L. Sprung, J. D. Sigetich, Hua Wu and J. Martorell, ``Bound states of a finite periodic potential,'' American Journal of Physics 68 715-722 (2000).

25

V. Aldaya and J. Guerrero, ``Canonical coherent states for the relativistic harmonic oscillator,'' Journal of Mathematical Physics 36 3191-3199 (1995).

January 9, 2001