next up previous contents
Next: Binary Octagonal Flexagon Up: Octagonal Flexagons Previous: Introduction

First Level Octagonal Flexagon


  
Figure 1: The first level octagonal flexagon has 8 vertices.
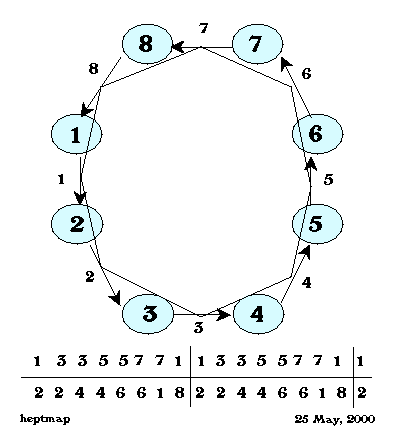
\begin{figure} \centering \begin{picture} (250,280) \put(0,0){\epsfxsize=250pt \epsffile{octmap.eps}} \end{picture} \end{figure}

Although there is some overlapping of the individual octagons in a strip of octagons, it is still not severe, and is outweighed by the versatility of thye resulting octagonal flexagon. In any event, it is the relationship between successive hinges which matters in a flexagon, so the remainder of the polygon can be rearranged to suit convenience or aesthetics.

If it is considered important to preserve the full symmetrical polygons, they can be cut out individually and pasted toggether. Once the strip is folded, overlapping will no longer be a problem. If rapidity and efficiency of assembly is preferrd, corners can be cut but the flexagon will still work.


  
Figure 2: Permutation of the octagons along the strip for a first level octagonal flexagon.
\begin{figure} \centering \begin{picture} (200,200) \put(0,0){\epsfxsize=200pt \epsffile{octper.eps}} \end{picture} \end{figure}


  
Figure 3: Top side of an octagonal flexagon consisting of one single cycle.
\begin{figure} \centering \begin{picture} (400,490) \put(0,0){\epsfxsize=400pt \epsffile{hoctatop.eps}} \end{picture} \end{figure}


  
Figure 4: Bottom side of an octagonal flexagon, consisting of one single cycle.
\begin{figure} \centering \begin{picture} (400,490) \put(0,0){\epsfxsize=400pt \epsffile{hoctabot.eps}} \end{picture} \end{figure}

next up previous contents
Next: Binary Octagonal Flexagon Up: Octagonal Flexagons Previous: Introduction
Microcomputadoras
2000-11-10