next up previous contents
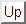
Next: Second Level Pentagonal Flexagon Up: Ternary Pentagonal Flexagon Previous: Cis-ternary pentagonal flexagon

Trans-ternary pentagonal flexagon


  
Figure 23: Map, with Tukey pentagons, of the trans-ternary pentagonal flexagon.
\begin{figure} \centering \begin{picture} (300,250) \put(0,0){\epsfxsize=300pt \epsffile{tnsterflenmap.eps}} \end{picture} \end{figure}


  
Figure 24: Permutation of the pentagons along the strip for a binary pentagonal flexagon. Three cycles are manifected by the three blocks in the permutation. That two of them result from recursive replacement manifests itself in the size and cyclic structure of two of the blocks.
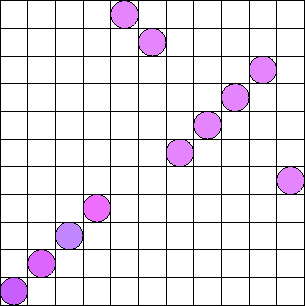\begin{figure} \centering \begin{picture} (200,220) \put(0,0){\epsfxsize=200pt \epsffile{tnsterflenper.eps}} \end{picture} \end{figure}


  
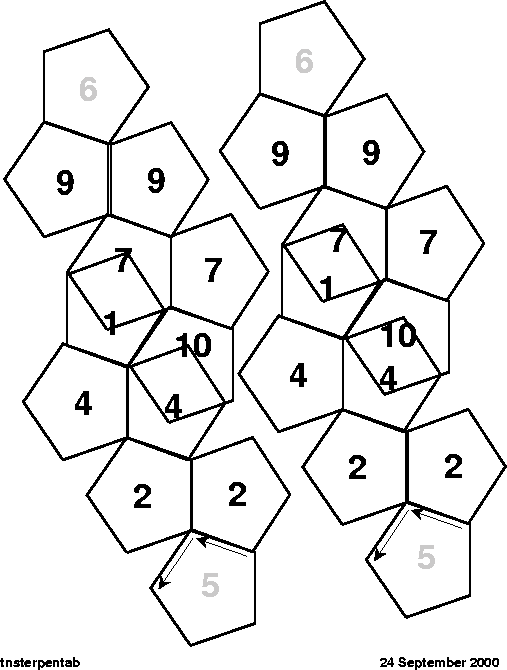
Figure 25: Top side of the trans-ternary pentagonal flexagon cutout. The flexagon has eleven faces. Because the number is odd, one of the sectors has to be turned over to get the other with a smooth match. The figure will make one flexagon.
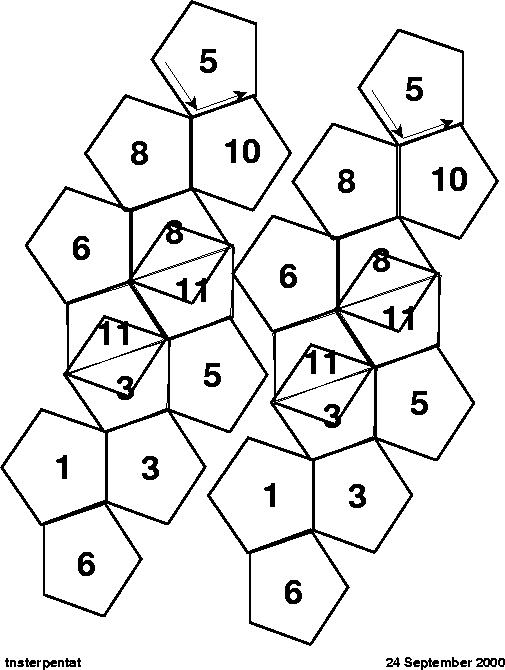\begin{figure} \centering \begin{picture} (360,440) \put(0,0){\epsfysize=440pt \epsffile{tnsterpentat.eps}} \end{picture} \end{figure}


  
Figure 26: Bottom side of the transs-ternary pentagonal flexagon cutout.
\begin{figure} \centering \begin{picture} (360,440) \put(0,0){\epsfysize=440pt \epsffile{tnsterpentab.eps}} \end{picture} \end{figure}


Microcomputadoras
2000-10-02