Differential Equation Theory

However, the real role of a differential equation lies in relating conditions in one region to those in another, through a recursive process which allows us to progressively work out the solution fiom one place to another, a little bit at a time. The framework is prescribed by the differential equation, but the information which is to be relayed from one place to another is contained in the boundary conditions. We need not grieve if the system is capable of sending more information than we shall ever attempt, which is another way of interpreting the fact that the differential operator may have eigenfunctions which do not belong to Hilbert space while we want to confine ourselves to square integrable functions. The other anomaly which may arise is that the system is incapable of transmitting cerlain information, or of transmitting it in certain ways. This would seem to be the failure which occurs for the strongly singular potentials.

Probably the most fundamental aspect of the whole theory of differential equations is the existence of a Green's formula. These are formulas which relate integrals invoking the solutions of a differential equation to its boundary values. The name is chosen because of the analogy to relations occurring in the early theory of electricity by which numerous volume integrals could be transformed into surface integrals These were introduced by Green in a pamphlet published in I828 [12].

From a mathematical point of view such integrals correspond to bilinear or quadratic forms. A Green's formula permits them to be expressed in terms of their boundary values, through a process akin to integration by parts. In terms of vector space concepts, the result is a mapping from a large-dimensional space which would be comprised of all possible functions, of which there is a subspace which is highly constrained consisting; of those functions which actually solve the differential equation. The mapping is from this rather small-dimensional subspace of possible solutions, which is embedded in a very much larger space, to the space of boundary values. The boundary values are in one-to-one correspondence with the solutions and are free from any constraints.

Bilinear forms and norms are very intimately related: in a Hilbert space they determine one another. It is through the mapping of a norm or the bilinear forms in function space to their counterparts in the boundary value space that the theory or operators on Hilbert space becomes involved in the solutions of differential equations. The crucial point to be observed is that the theory only relates the norms to one another, without in any way implying that the solutions of the differential equations have to belong to the Hilbert space. Misunderstanding of this point has been principally responsible for the conceptual difficulties surrounding continuum wave functions.

Bilinear forms are mapped from the solution space to the boundary value space in a rather curious way. Positive-definite bilinear forms become symplectic bilinear forms in the boundary value space. Because of its anti-Hermitian character a symplectic form vanishes identically for equal but purely real arguments. Should an equality between symplectic forms involve such arguments, it would he somewhat vacuous.

Two avenues for obtaining information are then open: one is to take limits, the other is to use complex solutions to the ditferential equation. The former approach leads to the classical Christoffel-Darboux formulas and a number of useful relationships involving derivatives of solutions. The complex approach allows us to use the full apparatus of complex variable theory, in particular the possibility of analytic continuation with respect to the eigenvalue parameter. It is found that the resulting class of functions is sufficiently interesting to warrant that line of approach.

Oddly enough, when we come to regard a differential equation as serving only to define a mapping from the solution space to the boundary value space, it is possible to avoid an excessive preoccupation with the actual boundary values themselves. Such a maneuver docs not avoid the formulation of boundary conditions, but it sets them aside into another category, and at the same time permits approximations to be made. This is yet another way to work with wave packets, which approximately solve the differential equation, or which approximately meet the boundary conditions, as most suits the convenience of the moment.

Among the functions which can be obtained with the help of a Green's formula, by far the most important of them all is the spectral density function. Such a function has been familiar to electrical engineers as the complex impedance of a continuous line, and to physicists as the Jost function or as the S-matrix. Strictly speaking the crucial function is the Titchmarsh-Weyl m function, whose imaginary part over the real axis is the spectral density. On account of its being the imaginary part of the boundary value of an analytic function, possibilities exist for its analytic continuation, to write dispersion relations for it, and for activities of a related nature. Such relations have been extensively studied by theoretical physicists in other contexts.

It is worth examining the derivation of the spectral density wilh some care, considering its importance for a general theory.

To begin with, the one-dimensional, time-independent Schrödinger equation can be written in the standard self-adjoint form

$$\begin{eqnarray*}\left\{-\frac{d}{dx}p(x)\frac{d}{dx}+q(x)\right\}\psi(x) & = & \lambda\psi(x) \end{eqnarray*}$$

Here $\psi(x)$ is the wave function, q(x) is the potential energy, while $\lambda$ is the energy, appearing in the equation in the role of an eigenvalue parameter. The weight function p(x), assumed always to be strictly positive, may arise sometimes from the separation of variables in non-Cartesian coordinate systems. Units of distance and energy have been so chosen that the purely physical constants do not make an appearance explicitly anywhere in the equation.

It is convenient to introduce the operator symbolism

$$\begin{eqnarray*}{\cal L}[\psi] & = & \lambda \psi \end{eqnarray*}$$

which can be used to summarize the differential equation which we have written, as well as eventually others, such as the one-dimensional Dirac equation.

Green's formula can be obtained from an integration by parts: it states that

$$\begin{eqnarray*}\int_a^b\{\varphi^*{\cal L}[\psi] - {\cal L}[\varphi]^*\psi\}dx & = & [\varphi,\psi]\vert _a^b. \end{eqnarray*}$$

The bracket, which we have indicated on the right-hand side of the equation, is defined by

$$\begin{eqnarray*}[\varphi,\psi](x) & = & -p(x)\{\varphi^*(x)\psi'(x)-\varphi'^*(x)\psi(x)\}. \end{eqnarray*}$$

It is somewhat more suggestive to write a self-adjoint second-order differential equation as a pair of coupled first-order equations, preferably in matrix form. We could then write

$$\begin{eqnarray*}\frac{d}{dx}\left(\begin{array}{c} \psi \\ p\psi' \end{array} \... ...ht) \left(\begin{array}{c} \psi \\ p\psi' \end{array} \right). \end{eqnarray*}$$

In turn we are permitted to write the bracket in the form

$$\begin{eqnarray*}[\varphi,\psi]& = & \left(\begin{array}{cc} \varphi^* & \varp... ...ght) \left(\begin{array}{c} \psi \\ \psi' \end{array} \right). \end{eqnarray*}$$

Given such a representation, it is quite clear that the bracket is a bilinear form defined by an antisymmetric metric matrix. Let us adopt a quaternionic notation for the $2\cdot 2$ Pauli matrices:

$$\begin{array}{ccc} \begin{array}{c} {\bf 1}= \left( \begin... ... & 1 \end{array} \right) = {\bf k}^t \end{array} \end{array}$$

By doing so we can incorporate the one-dimensional Dirac equation into this same scheme of notation. According to Coulter and Adler [13] we might write such an equation in the form

$$\begin{eqnarray*}\frac{d\psi}{dx} & = & (E{\bf j}- V{\bf i}+m_o{\bf i})\psi \end{eqnarray*}$$

with energy E, potential energy V, and rest mass m₀. $\psi$ is now a two-component vector.

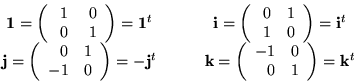
Define the operator ${\cal L}$ by

$$\begin{eqnarray*}{\cal L}\psi & = & \left(-{\bf j}\frac{d}{dx} + V {\bf 1}- m_0{\bf k}\right)\psi \end{eqnarray*}$$

Supposing that the inner product in the solution space for the Dirac equation involves the sum of the absolute squares of both components, we can deduce a Green's formula

$$\begin{eqnarray*}\int_a^b\{\varphi{\cal L}\psi - ({\cal L}\varphi)^t \psi\}dx & = & -\varphi^t{\bf j}\psi\vert _a^b. \end{eqnarray*}$$

Again, the presence of the antisymmetric metric matrix assures us that the boundary values will follow a symplectic geometry.

The Dirac equation for three-dimensional, spherically symmetric potentials can be cast into a rather similar form, once the angular variables have been separated. The radial equation which remains consists of the same pair of coupled first-order equations which arises for the one-dimensional Dirac equation.

Regardless of the context, the derivation of a Green's formula, which primarily involves inventing an appropriate anti-Hermitian form for the boundary space, is a crucial step. Once such a formula is available, the remaining steps in the derivation which we shall outline forthwith remain virtually unchanged, whatever the differential equation which is under discussion. It is fortunate that it is possible to discover an adequate formula in the widest variety of situations. Roos and Sangren [14] have shown how the brackets may be obtained for the pair of equations corresponding either to the one-dimensional Dirac equation or the radial part of the three-dimensional Dirac equation. Their procedure is much as we have discussed it above. Kodaira [15] has obtained a bracket for a differential operator of arbitrary even order while Everitt [16] has studied the particular case of fourth-order operators quite exhaustively. Similar constructions are possible for systems of differential operators, as well as for partial differential operators. Green's formula is particularly effective when it is applied to eigenfunctions of the differential operator from which it was derived. Supposing that

$$\begin{array}{cc} \begin{array}{ccc} {\cal L}[\varphi] & = ... ...}{ccc} {\cal L}[\psi] & = & \mu \psi, \end{array} \end{array}$$

we obtain

$$\begin{eqnarray*}(\mu - \lambda^*)\int_a^b\varphi^*\psi dx & = & [\varphi,\psi](b) - [\varphi,\psi](a) \end{eqnarray*}$$

Using the traditional parentheses to denote an inner product in the solution space, this equation finally relates the two bilinear forms: the parentheses in the solution space and the brackets in the boundary value space.

A particularly important case results when $\lambda^* = \mu$, which will occur whenever both $\varphi$ and $\psi$ belong to the same eigenvalue, tempting us to apply Green's formula to $\varphi^*$ and $\psi$. In such a case. the left-hand side of the equation uses the real inner product in the solution space, which does not matter because it has a zero multiplier of the form $\lambda - \lambda$.

If we define

$$\begin{eqnarray*}W[\varphi,\psi] & = & [\varphi^*,\psi], \end{eqnarray*}$$

we obtain, for functions belonging to the same eigenvalue of ${\cal L}$,

$$\begin{eqnarray*}W[\varphi,\psi](a) & = & W[\varphi,\psi](b), \end{eqnarray*}$$